Fourier Analysis is the decomposition of any square-integrable functions into an infinite series of trigonometric functions. Here we show that the trigonometric polynomial functions are dense in the space of periodic continuous functions, and thus can be used as good approximations. This implies that any repeating pattern-as-function, however complex, as long as having continuity, has a series of simple trigonometric functions that will approximate it within a given error-tolerance.
We begin thus with some definitions:
- A subset
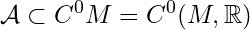 , the space of continuous real functions from any metric space
, the space of continuous real functions from any metric space  , is a function algebra if it is closed under addition, scalar multiplication, and function multiplication, i.e.
, is a function algebra if it is closed under addition, scalar multiplication, and function multiplication, i.e. 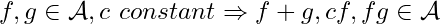 .
. 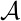 vanishes at point
vanishes at point 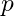 if
if 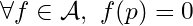 .
.
Note: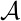 Non-Vanishing in
Non-Vanishing in 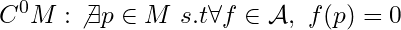 , i.e.
, i.e. 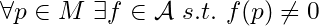 .
.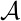 separates points if
separates points if 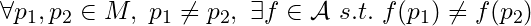 . \
. \
Note: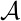 Separates
Separates 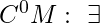 a countable collection of
a countable collection of  are dense in
are dense in 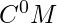
- a trigonometric polynomial is defined by:
![Rendered by QuickLaTeX.com \[T(x)=a_0 + \sum_{k=1}^{n}a_k \sin kx + \sum_{k=1}^{n}a_k \cos kx\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-57d50e525d9246f460a61706041ab386_l3.png)
Note: the function algebra of all trigonometric polynomials,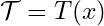 separates points of
separates points of 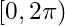 and vanishes nowhere
and vanishes nowhere
The Stone-Weierstrass Theorem: If  is a compact metric space and
is a compact metric space and 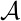 is a function algebra in
is a function algebra in 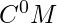 that vanishes nowhere and separates points, then
that vanishes nowhere and separates points, then 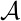 is dense in
is dense in 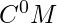
i.e. 
Note: We can see immediately that  is dense in the periodic functions on
is dense in the periodic functions on 
Lemma 1: If 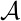 vanishes nowhere and separates points then
vanishes nowhere and separates points then  with specified values at any pair of distinct points, i.e.
with specified values at any pair of distinct points, i.e. 
since
![]() vanishes nowhere, there must at least a function for each point not equal to 0 at that point, i.e.
vanishes nowhere, there must at least a function for each point not equal to 0 at that point, i.e. . Since
![]() is an algebra,
is an algebra, and is non-zero at either point, i.e.
. Since
![]() separates points, let
separates points, let be a separator of these two points, i.e.
. Thus, there is a linear combination of
and
with the specified values:
Letting 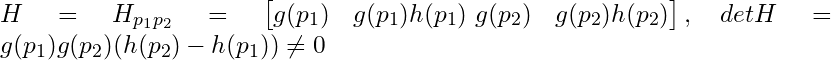
, i.e. there is a linear solution, implying that
is the specified function with
.
Lemma 2: The closure of a function algebra in  is a function algebra
is a function algebra
it follows that
, which is thus closed under addition, function multiplication, and scalar multiplication, and so a function algebra.
Proof of the Stone-Weierstrass Theorem: 
Prove: by approximating the absolute value function on the interval
by a polynomial.
From the Weierstrass Approximation Theorem: since is a continuous function, on
polynomial
that approximates it, in that
The closures of a function algebra is closed under absolute value, minimum, and maximum operations.
Let, which has a zero constant term, yet still approximates
since
from Weierstrass Approximation Theorem so
. Writing
and
as an approximation of
, by Lemma 2
is an algebra so
since
has no constant term and can thus be generated by the 3 closed function algebraic operations. With
by the sequence of
approximations with
. Since
and by repetition, so are the max \& min for a finite number of functions.
 separates
separates  : Due to compactness of M,
: Due to compactness of M, for which the linear combination of the product of their separating and non-vanishing functions (
) are dense in
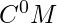
, by Lemma 1,
.
(i) Fixing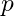 and letting
and letting vary, since
are continuous (i.e.
), so is
, and thus because
neighborhood around q such that for
. Since
 is compact and
is compact and , a finite subcover. Defining
, since
for some
for some
.
(ii) Now repeating the above for variable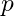 ,
, is continuous with
neighborhood around p such that for
, a finite subcover. Setting
and since
for some
for some
.
Fromsince
for some i and
, therefore
. Thus, from
.
A corollary of the Stone-Weierstrass Theorem: Any  -periodic continuous function of
-periodic continuous function of  can be uniformly approximated by a trigonometric polynomial
can be uniformly approximated by a trigonometric polynomial
\[T(x)=a_0 + \sum_{k=1}^{n}a_k \cos kx + \sum_{k=1}^{n}a_k \sin kx]\![]() parameterizes the unit circle
parameterizes the unit circle by
. Since
is compact, a
-periodic continuous function of
is equivalent to a continuous function on
. The trigonometric functions
are an algebra. If
, so
vanishes nowhere. And,
so it separates points. Thus, by the Stone-Weierstrass Theorem, the trigonometric polynomials
are dense in
.
This result may be extended to any p-periodic function by changing the trigonometric polynomial class
\[T_p(x)=a_0 + \sum_{k=1}^{n}a_k \cos \frac{k}{r}x + \sum_{k=1}^{n}a_k \sin \frac{k}{r}x, \ r=\frac{p}{2\pi}]\
Fourier Analysis
The Trigonometric Functions are an orthonormal basis to
and so their linear combinations with

References
- Pugh, Real Mathematical Analysis, pp. 234-239.
- Elias M. Stein & Rami Shakarchi, Real Analysis: Measure Theory, Integration, \& Hilbert Spaces. Princeton Lectures in Analysis, Vol. III, pp. 160,170,171.

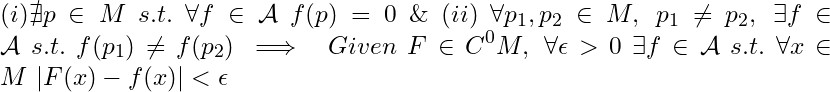
![Rendered by QuickLaTeX.com |q(y)-|y||=|p(y)-|y|-p(0)|< |p(y)-|y||+|p(0)-|0||<\epsilon/2 + \epsilon/2 =\epsilon \ \forall y \in [-||f||,||f||]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-de35e53e6769fe486c71d30c50e539c1_l3.png) . Writing
. Writing 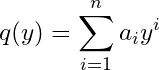 and
and 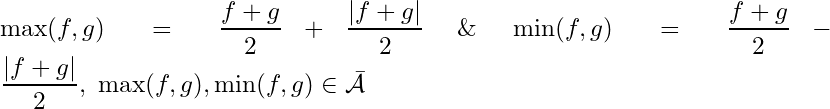 and by repetition, so are the max \& min for a finite number of functions.
and by repetition, so are the max \& min for a finite number of functions.