Definition
The logarithm function is one of the most known and used functions in mathematics and other fields like physics, finance, chemistry, …etc. this article is logarithmic heaven where you can learn many things about logarithmic functions and where you can find a large list of logarithm rules, identities, and formulas gathered in one place to make easy the manipulation and the evaluation of the various calculations that involve logarithms. So let’s start our journey in the logarithm world!!!
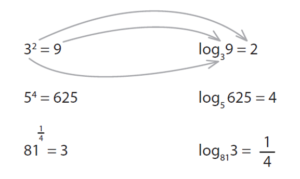
All you need to know is that logarithms are essentially a different format for writing exponents. If you know how to use exponents and you know the format for logarithms, then you’ll do fine in this section.
Let’s take an example:
If log464 = x, then what is the value of x?
Virtually every major test contains some variation on this problem, so plan ahead to make sure you know how to answer this problem type.
You’ll be given a logarithm problem with one value (x, y, or z) missing. All you need to do is rewrite that sucker as an exponential statement. Take a look!
We’re given: log464 = x
Rewritten: 4x = 64
That’s a lot easier to work with, isn’t it? Find matching bases and you’re practically done!
4x = 43
x = 3
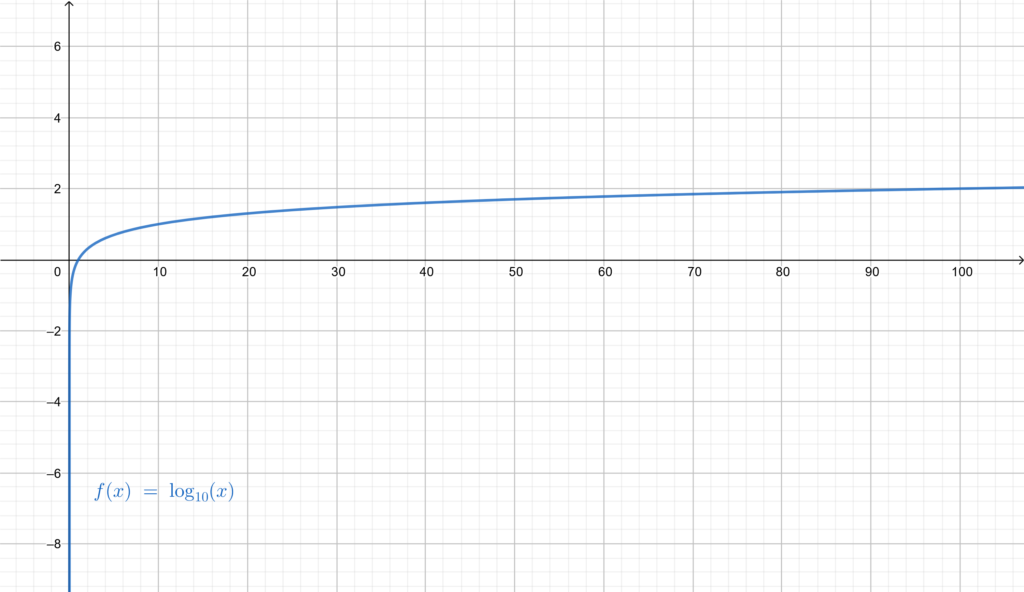
Common logarithm
We call “Common logarithm” the logarithm function with the base 10. Generally noted by “” or “
”. It is also known as the “decadic logarithm” and as the “Decimal logarithm”, and also known as the “Briggsian logarithm” in honor of the British mathematician Henry Briggs how was notable for changing the original logarithms invented by John Napier into the logarithm with base 10.
The common logarithm of is the power to which
would have to be raised to equal
, meaning that common logarithm
is the inverse of the exponential function
.
Graph of the common logarithm
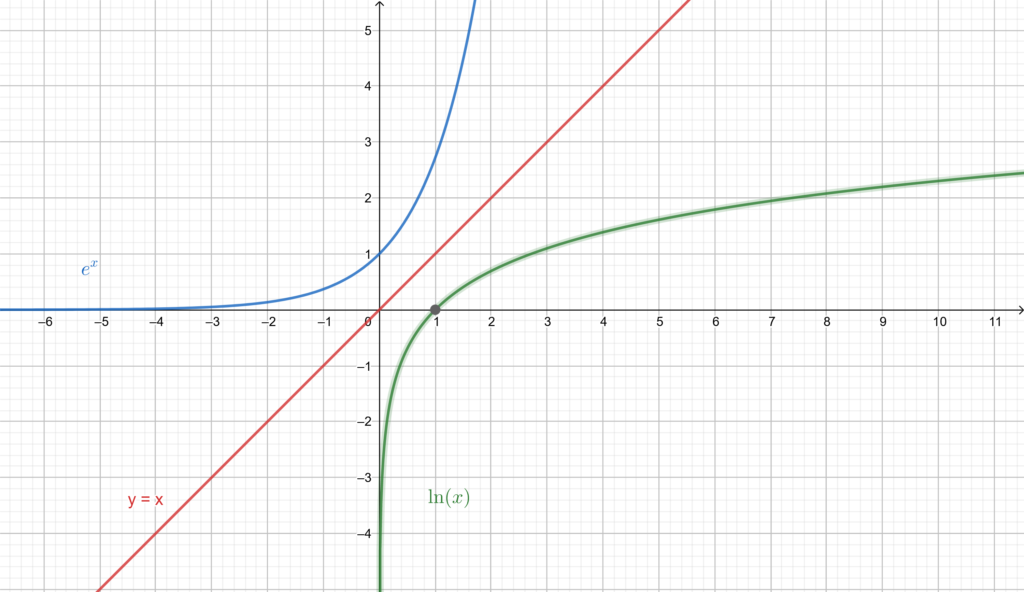
Natural logarithm
While the common logarithm has a base 10, the Natural logarithm has a base , where
is the mathematical constant known as “Euler’s number” or “Napier constant”; it is an irrational and transcendental number, its value is approximately
, this constant is also widely used as a base for exponential functions. Natural logarithm is noted
or
. The natural logarithm of
is the power to which the constant
would have to be raised to equal
, meaning that the natural logarithm
is the inverse of the exponential function
.
Here is Graph of the natural logarithm and the exponential function
. Note the natural logarithm and the exponential function base
are symmetrical with respect to the line
.
Common and natural logarithms can be expressed in terms of each other as follow:
Logarithm Rules, identities, and formulas
1- Logarithm of the base: because
2- Logarithm of 1: because
Logarithm identities for canceling exponentials:
3- because
4- because
Logarithm identities for the different operations:
5- Logarithm of product: because
6- Logarithm of the reciprocal:
7- Logarithm of a quotient: because
8- Logarithm of the reciprocal of a power of base:
9- Logarithm of a power:
10- Logarithm of a square root:
11- Logarithm of the n root:
12- Logarithm to a quotient base:
13- Logarithm to a power base:
14- Logarithm of a power to a power base:
15- Power with an logarithmic exponent to the same base as the power:
16- Power with a logarithmic exponent: because
17- Since the logarithm is a monotonic function, more precisely monotone increasing function if the base and monotone decreasing function if the base
, therefore we have:
18- Logarithm with the base is the Natural Logarithm
19- Logarithm transitive property:
20-
21-
22-
23- For
are real positive numbers and
and
and
are real numbers; because
24-
25-
Changing the logarithm base:
26- Changing the logarithm base:
This identity of changing the base is very useful to calculate the wanted logarithm using the calculators, espacealy useful since nearly all calculators have a “” and an “
” buttons, but not all of the calculators have a button for a logarithm with a random base.
27- The formula of base changing has many consequences, from which we cite:
Where is any permutation of the subscript
. For example:
28- Changing the natural logarithm (base ) to the common logarithm (base 10):
29- Switching the logarithm base with the logarithm argument:
30- From the previous one we can write also: (Canceling logarithm by multiplying by the logarithm with the base and the argument switched)
Summation and subtraction identities: This two identities are especially useful in probability theory, when dealing with logarithmic probabilities:
31- because:
32- because:
with
(or else the subtraction identity won’t be defined since the logarithm of 0 doesn’t exist).
33- More generally:
Some useful exponent identities:
34-
35-
Some other identities:
36-
37-
Common mistakes that you should avoid and be careful from:
- The log of a sum isn’t the sum of the logs, because the sum of the logs is the log of the product, and the log of a sum can’t be simplified.
- Also, the log of a sum isn’t the product of the logs, it is tricky if you are not careful since it is close to the logarithm product rule.
- The product of the logs isn’t the log of the product.
- The log of a difference isn’t the difference of the logs, the difference of the logs is the log of the quotient, and the log of the difference same as the log of the sum can’t be expressed in a simpler way.
- Also, the log of the difference isn’t the quotient of the logs, its the opposite that is true, the log of a quotient is the difference of the logs.
- The exponent to which the log is raised to a power of, isn’t the coefficient of the log; the logarithm raised to a power can’t be simplified.
- The log of a quotient isn’t the quotient of the logs.
Limits of the logarithm function:
38- Logarithm of 0: is undefined;
We have:
39- when tend to infinity:
40-
41- 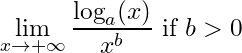
this limit is usually summarized and made easy to memorize by the expression “Logarithms grow more slowly than any power or root of “.
Derivatives of logarithm functions:
With , and
, We have:
42-
43-
Integrals of logarithmic function:
44- Integral definition:
45-
46-
47- For higher-order integrals, it is convenient to define: , where
is the n
harmonic number.
and so we get:
Therefore:
َAbsolute value:
When dealing the logarithm, we need to keep an eye on the signs and the values of the base and the argument of the logarithm function, we can summarize the conditions we have to verify as follow:
We have the definition of logarithm:
- The base
can’t equal 1,
- The base
can’t be negative,
- The argument of the logarithm function
can’t be less or equal to 0.
These conditions must be taken into consideration when with real numbers, and to do so we use the absolute value when necessary to ensure that the conditions are always met.
In the case of real numbers, we introduce the absolute value to some of the logarithm rules, as follow:
48-
49-
50-
Complex logarithm:
51- The logarithm to the real base of a negative number
is undefined.
For complex number in the polar form:
Then the complex logarithm for negative is given by:
Taking in account periodicity we can write:
we find:
52-
53-
54-
55- for
56- 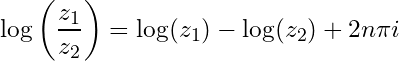
57- for
58- for
59- for
and
60-
61- (mod
)
62- with
63- with
64- with
65- 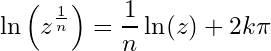
Why not take a look at the 3D plot and the contour plot of the logarithm and the exponential functions!!!
Logarithmic inequalities:
66- If
67- If
68- If
69- If
70- If
71- If
72- If
73-
74-
75-
Here is a summary of the main rules of the logarithm
Some solved examples:
- If 64 = x2 then logx64 = ?
Here, x = 8
So, log864 = log882 = 2
- 2 log24 + log2x =-1, then x = ?
Here, log242 + log2x = -1
log2 ( 16x) = -1
16 x = 2-1
16x = ½
x = 1/32
- log216y= 1/3, what is the value of y ?
y = 2161/3
y=6
- If logx9 – logx4 = 1/2, then x = ?
logx (9/4) = ½
9/4 = x1/2
Squaring both sides,
x = 81/16
Convert these expressions into logarithms
- 83 = 512
- 72 = 49
- 6x = 216
(Answers at the bottom of the article)
Solve these logarithms for the missing info:
- log381 = x, then x = ?
- If logx196 = 2, then x = ?
- If log2(x) = 5, then x = ?
(Answers at the bottom of the article)
Characteristic & Mantissa
The logarithm of a number has an integral part and a decimal part. The integral part is called the characteristic and the decimal part is called the mantissa.
For example, log10 91000
= log10 (104 x 9.1)
log10 104 + log10 9.1
= 4 + 0.959
Here, 4 is the characteristic and 0.959 is the mantissa.
Number of digits
A significant property of the characteristic (for common logarithms) is that (characteristic + 1) will give the number of digits of the integral part of the number whose logarithm you determined. In the above example, 91000 contains (4 + 1) = 5 digits.
This is explained as follows:
log10 91000 = 4.959,
91000 = 104.959 = 104+ 0.959 = 104 100.959
= 10x 10y
Since y will always be < 1, 10y will always be < 10. Hence, the number of digits in the number will be equal to the number of digits in 10x, which in turn is equal to (x + 1).
Also, the characteristic of a logarithm could be either positive or negative; however, the mantissa should always be positive.
For example, log10 0.091 = log10 (10–2 9.1)
–2 + 0.959 =
If the calculated value of the logarithm of some number is negative (usually, calculators generate values containing a negative mantissa), then we make the mantissa positive as follows:
–1.041 = –(1 + 0.041) = –1 – 0.041
= (–1 – 1) + (–0.041 + 1)
= –2 + 0.959
Antilogarithm
We call “Antilogarithm” the inverse of the logarithm function, and we write as follow:
, in other words and to put it simply the antilogarithm is the exponentiation! For example the antilogarithm of is
, and the antilogarithm of
is
.
Note that since each function is the inverse of the other then we have the .
For example, the antilogarithm of in base
is
Cologarithm
We call “Cologarithm” the logarithm of the reciprocal of a number , which is, using the logarithm properties, equal to the negative of the logarithm of this number, we can write as follow:
Harmonic logarithm
We call “Harmonic logarithms” of order and degree
, the unique functions that, for all integer
(
) and for all non-negative integer
(
), verify the following:
-
,
has no constant term except
,
,
Where the “Roman symbol” is defined by
This gives the special cases:
Where is a Harmonic Number:
The harmonic logarithm has the Integral
The harmonic logarithm can be written
Where is the Differential Operator, (so
is the
integral). Rearranging gives
This formulation gives an analog of the Binomial Theorem called the Logarithmic Binomial Formula. Another expression for the harmonic logarithm is
Where is a Pochhammer Symbol and
is a two-index Harmonic Number.
References
- Loeb, D. and Rota, G.-C. “Formal Power Series of Logarithmic Type.” Advances Math. 75, 1-118, 1989.
- Roman, S. “The Logarithmic Binomial Formula.” Amer. Math. Monthly 99, 641-648, 1992.
Logarithmic Series
We can express and expand some logarithm expressions as a series of powers of , if we have
Let’s take a look at some logarithm series
- We can write an expansion of
if
as follow:
Then we can deduce the expansion of by replacing
with
and we will get:
Or in other way:
Now let’s take a look at some results derived from the previous series using the properties of the logarithmic function
- The previous algorithmic series isn’t valid if
but what if
? Well, it is proved that logarithmic series is valid also for
, and we get the following:
Note that the logarithm series isn’t valid when and it doesn’t have a sum, and this makes sense since
isn’t a finite quantity.
- If we look at the differences between the exponential series and in comparison with the logarithmic series we find that the exponential series is expressed by the sum of positive terms (positive signs) but the terms of the logarithmic series are alternatively positive and negative.
Also the logarithmic series is valid only when whereas the exponential series is valid for every value of
.
- Some examples of Infinite series of various simple functions of the logarithm:
Where represent the Euler-Mascheroni constant and
is the Riemann zeta function.
False Logarithmic Series
We call False logarithmic series the function expressed as follow:
This function is interesting since it gives the same image of the logarithmic function for every natural number, i.e. , or in other terms the graph of the false logarithm function
intersect with the graph of the logarithm function for every
such that $x\in\mathbb{N^{*}}.
Here is a graphical representation of the false logarithm function and the logarithm function, notice the intersection points of the two graphs.
Things to remember
- Logarithms are generally expressed to the base 10. These are called common logarithms. If no base is mentioned, it is assumed that the base is 10.
- Logarithms are not defined for zero or negative numbers. They are defined only for positive numbers.
- Logarithms can be expressed in any base.
- Logarithms expressed in one base can be converted to logarithms expressed in any other base.
Logarithm Quotes
The spectacular thing about Johnny [von Neumann] was not his power as a mathematician, which was great, or his insight and his clarity, but his rapidity; he was very, very fast. And like the modern computer, which no longer bothers to retrieve the logarithm of 11 from its memory (but, instead, computes the logarithm of 11 each time it is needed), Johnny didn’t bother to remember things. He computed them. You asked him a question, and if he didn’t know the answer, he thought for three seconds and would produce an answer. — Paul R. Halmos
Imagine a person with a gift of ridicule [He might say] First that a negative quantity has no logarithm; secondly that a negative quantity has no square root; thirdly that the first non-existent is to the second as the circumference of a circle is to the diameter. — Augustus de Morgan
You have no idea, how much poetry there is in the calculation of a table of logarithms! — Carl Friedrich Gauss
Answers:
- 83 = 512 ; log8512 = 3
- 72 = 49 ; log749 = 2
- 6x = 216 ; log6216 = x
- log381 = x, then x = ? 4
- If logx196 = 2, then x = ? 14
- If log2(x) = 5, then x = ? 32
Conclusion:
Well, here we arrive at the end of this journey in this logarithmic paradise if you have anything you want to be added to this article just let us know, and we will make sure to add it to make this article the ultimate logarithmic article. Also, make sure to check the blog post about Absolute Value and Logarithms.
And don’t forget to join us on our Facebook page stay updated on any new articles and a lot more!!!!!

![Rendered by QuickLaTeX.com \[\ln x =\dfrac{\log_{10}x}{\log_{10}e} \, \, ; \,\, \log_{10}x=\dfrac{\ln x}{\ln 10}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-6c28537a5e0052dd2ca4d43402bdf7f9_l3.png)
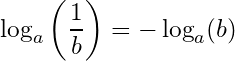
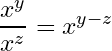
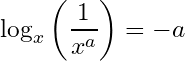
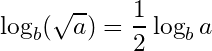
![Rendered by QuickLaTeX.com \log_{b}(\sqrt[n]{a})=\log_{b}(a^{\frac{1}{n}})=\dfrac{1}{n}\log_{b}a](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-55818985ec8e719e168fb2e43eb7ec06_l3.png)
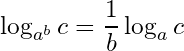
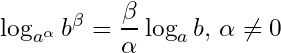
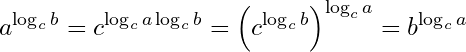
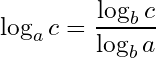
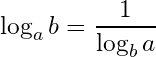
![Rendered by QuickLaTeX.com \[\log_{b}\sum_{1=0}^{N}a_{i}=\log_{b}a_{0}+\log_{b}\left( 1+\sum_{i=1}^{N}\dfrac{a_{i}}{a_{0}}\right)=\log_{b}a_{0}+\log_{b}\left( 1+\sum_{i=1}^{N}b^{(\log_{b}a_{i}-\log_{b}a_{0})}\right)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d885db6957c9e79bd205dd91c55ecffc_l3.png)
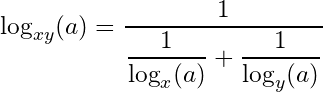
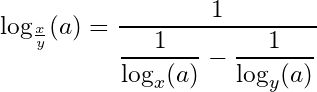
![Rendered by QuickLaTeX.com \[\log_{c}(a-b)\neq\dfrac{\log_{c}(a)}{\log_{c}(b)}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-7b434f36671cf016d6e9314ac1906cd2_l3.png)
![Rendered by QuickLaTeX.com \[\log_{c}\left(\dfrac{a}{b}\right)\neq\dfrac{\log_{c}(a)}{\log_{c}(b)}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-18bc947aefc894dd509ce470a8e17d2e_l3.png)
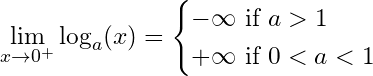
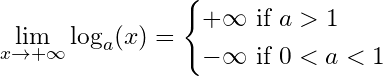
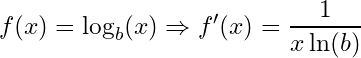
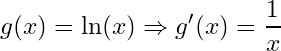
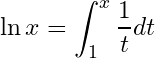
![Rendered by QuickLaTeX.com \begin{align*} x^{[0]}& =\log x\\ x^{[1]}& =x\log (x) -x\\ x^{[2]}& =x^{2}\log(x)-\dfrac{3}{2}x^{2}\\ x^{[3]}& =x^{3}\log(x)-\dfrac{11}{6}x^{3} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-fa81ed196b14d6e405a10e1b509cf1eb_l3.png)
![Rendered by QuickLaTeX.com \[\dfrac{d}{dx}x^{[n]}=nx^{[n-1]}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-0fe2a89af636e444bd62b334621791f7_l3.png)
![Rendered by QuickLaTeX.com \[\displaystyle \int x^{[n]}dx=\dfrac{x^{[n+1]}}{n+1} + C\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-17ec353397b9136f43539420ebd1c6c3_l3.png)
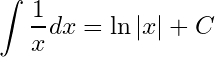
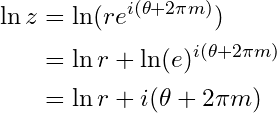
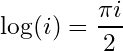
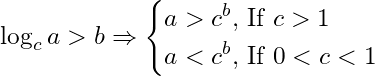
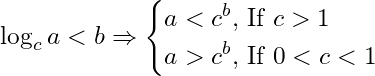
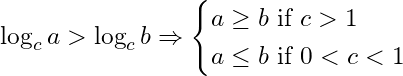
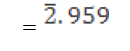
![Rendered by QuickLaTeX.com \[\text{colog}(x)\equiv\log\left(\dfrac{1}{x}\right)=-\log (x)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-dfc044daddb7b1b96d7376d9ad80dc9f_l3.png)
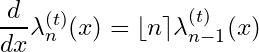 ,
,![Rendered by QuickLaTeX.com \[\lfloor n \rceil\equiv\begin{cases} n \text{ for } n\neq 0 \\ 1 \text{ for } n=0 \end{cases}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-3f27685b2177bba32c882fd670230588_l3.png)
![Rendered by QuickLaTeX.com \[\lambda_{n}^{(0)}(x)=\begin{cases} x^{n} \text{ for } n\geq 0 \\ 0 \text{ for } n<0 \end{cases} \]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8ac9ec9f406edc3306f1464f6cb39161_l3.png)
![Rendered by QuickLaTeX.com \[\lambda_{n}^{(1)}(x)=\begin{cases} x^{n}(\ln x-H_{n}) & \text{ for } n\geq 0 \\ x^{n} & \text{ for } n<0 \end{cases} \]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5d174a8355e7bd988710ab9f6aba0dd1_l3.png)
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\dfrac{1}{k} \]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1276fc58dbee1e55c857523a1e8c6b33_l3.png)
![Rendered by QuickLaTeX.com \[\int \lambda_{n}^{(1)}(x)dx = \dfrac{1}{\lfloor n+1 \rceil}\lambda_{n+1}^{(1)}(x) \]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-39bd47369d49a2519071cc3087813b43_l3.png)
![Rendered by QuickLaTeX.com \[\bar{D}^{k}\lambda_{n}^{(t)}(x)=\left\lfloor\dfrac{\lfloor n \rceil!}{\lfloor n-k \rceil}\right\rceil!\lambda_{n-k}^{(t)}(x).\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8e66fc44429933c1bf7c4ecbadd8ae3d_l3.png)
![Rendered by QuickLaTeX.com \[\lambda_{n}^{(t)}(x)=x^{n}\sum_{j=0}^{t}(-1)^{j}(t)_{j}c_{n}^{(j)}(\ln x)^{t-j}, \]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-7ab300239060e7e6c1e5a13f0654dc83_l3.png)
![Rendered by QuickLaTeX.com \[\log_{e}(1+x)=x-\dfrac{x^{2}}{2}+\dfrac{x^{3}}{3}-\dfrac{x^{4}}{4}+\cdots\infty\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-3ec352b903afdafb6d468539c21049eb_l3.png)
![Rendered by QuickLaTeX.com \[\log_{e}(1-x)=-x-\dfrac{x^{2}}{2}-\dfrac{x^{3}}{3}-\dfrac{x^{4}}{4}-\cdots\infty\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9a90f46ed9194b8766118cab1d917dc7_l3.png)
![Rendered by QuickLaTeX.com \[-\log_{e}(1-x)=x+\dfrac{x^{2}}{2}+\dfrac{x^{3}}{3}+\dfrac{x^{4}}{4}+\cdots\infty\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9bc4e1e846c438e2527a4150c6aace06_l3.png)
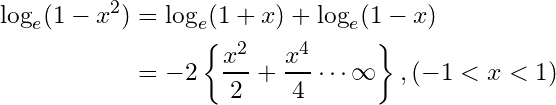
![Rendered by QuickLaTeX.com \begin{align*} \log_{e}(\dfrac{1+x}{1-x}) & =\log_{e}(1+x)-\log_{e}(1-x)\\ & =-2\left[ x+\dfrac{x^{3}}{3}+\dfrac{x^{5}}{5}+\cdots\infty \right], (-1<x<1) \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b736a5e76bb197e89ae9124a641221a0_l3.png)
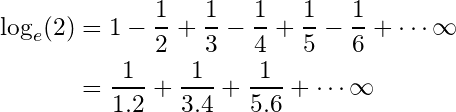
![Rendered by QuickLaTeX.com \[e^{x}=1+\dfrac{x}{1!}+\dfrac{x^{2}}{2!}+\dfrac{x^{3}}{3!}+\cdots\infty\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-03e68e1a5d7eb78d0350a14a2bcd6ff1_l3.png)
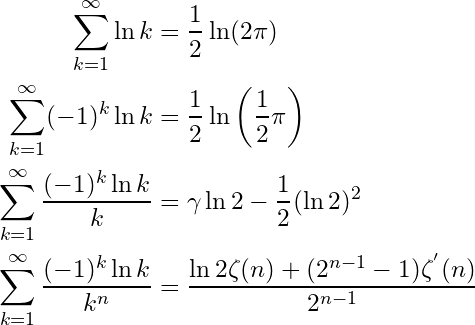
![Rendered by QuickLaTeX.com \[s_{a}(x)=\sum_{n=1}^{\infty}\left[ \dfrac{1}{1-a^{n}}\prod_{k=0}^{n-1}(1-xa^{-k}) \right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-948944c65e36db85b78b06370d54c297_l3.png)