INTRODUCTION
The study of a special type of series whose terms are trigonometric functions of a variable was started in the 18th century when J.B.J. Fourier (1768-1830) was successful in his attempt to prove that an arbitrary function given in the interval can be expressed under certain conditions in a trigonometric series of the form
and subsequently, such type of special series is given the name ‘Fourier Series’. It has great importance in the study of many branches of science including social sciences. The knowledge of Fourier series provides a powerful technique for solving problems of a periodic nature which occur in situations like theory of conduction of heat, electrical and mechanical vibrations, propagation of electromagnetic waves, acoustics, optics, etc. Fourier was the first person to initiate an elaborate study of trigonometric series and afterwards Dirichlet, Parseval, Bessel and many other mathematician made major contributions to the study of conditions of a function to be represented in a trigonometric series, convergence, integration, and differentiation of the Fourier series. In this article we are going to study Fourier series and their properties.
Before starting the article of Fourier series, it is essential to study the behaviour of periodic functions, piecewise monotone and piecewise continuous functions and some properties related to them.
PERIODIC, PIECEWISE MONOTONE AND PIECEWISE CONTINUOUS FUNCTIONS
Definition: Let , a function
is said to be periodic if there exists a positive constant
such that
for all
; the least number
possessing this property (if such a number exists) is called the period of the function.
is called periodic of period or fundamental period
.
is periodic of period
implies also
for all
.
The trigonometric functions ,
are periodic of period
and
,
are periodic of period
.
is periodic of period
Every constant function is trivially periodic with no definite Fundamental period.
The following observations are quite clear from the definitions of periodic functions.
- If
is defined on an interval of length
then
can be extended to the whole of
by making
periodic of period
.
- The graph of a periodic function over
will be replicas of a portion over an interval of length
if
is period of the function.
Hence if a function is defined on
it can be made to be a periodic function on
of period
. In fact, sum of two periodic function of same period is also a periodic function of that period.
If is periodic of period
then the following results are quite easy to prove:
Definition: A function is said to be piecewise monotone if there exists a partition of
into open sub-intervals in each of which
is monotone.
Every monotone function is piecewise monotone but the converse is not true.
For example
is piecewise monotone on [0, 1], but is not monotone on [0, 1].
Definition: A function is said to be piecewise continuous if there exists a partition of
into open sub-intervals in each of which
is continuous.
Every continuous function is piecewise continuous but the converse is not true.
For example, the function defined on
by
is piecewise continuous, since it is continuous on
,
,
, but is not continuous on
;
and
are points of discontinuities of
on
.
Theorem 2.1.
Definition (Fourier Series): Let be an integrable function on
or if
is unbounded on
, let the improper integral
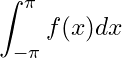
Then the trigonometric series
is called the Fourier series in corresponding to the function
, where
, called Fourier Coefficients, are given by
Definition: A sequence of Riemann integrable functions defined on
is called orthogonal if
and it is said to be orthonormal if
From Theorem 2.1, it easily follows that 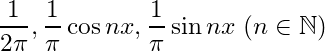
. The function
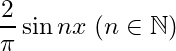
FOURIER SERIES EXPANSION
Not every function can be expanded into Fourier series. There are certain conditions which are to be satisfied by a function for its expansion into Fourier series. The most familiar one is Dirichlet’s conditions.
Dirichlet’s Conditions
Let be a given function.
is said to satisfy the Dirichlet’s conditions in
if it satisfies one of the following two conditions:
is bounded on
and the interval
can be broken into a finite number of open sunintervals of
, in each of which
is monotone i.e., in other words
is bounded and piecewise monotone on
;
has a finite number of points of infinite discontinuities on
but when arbitrarily small neighbourhoods of these points of discontinuities are excluded from
,
is bounded and piecewise monotone in the remainder of the interval
and also the improper integral
is absolutely convergent.
Remark: Dirichlet’s conditions can also be put in a slightly different form:
is said to satisfy Dirichlet’s condition on
if
is a function of bounded variation on
or when
has a finite number of points of finite discontinuities on
and when arbitrarily small neighbourhoods of these points are excluded from
,
is a function of bounded variation on the reminder of
and
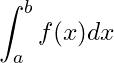
.
Theorem 3.1.
If the series 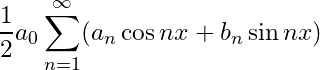
on
then it is the Fourier series for
in
.
Proof. Since the series 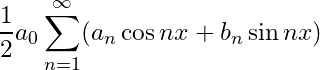
on
,
is the sum function of the series and we can write
(1)
By integrating term-by-term on , we get using Theorem 2.1,
Multiplying (1) by on both sides and integrating term-by-term (which is valid, since
is a bounded function and after multiplication the series is still uniformly convergent on
, we have
Multiplying (1) by on both sides and integrating term-by-term, we have
Hence, from definition the series (1) represents the Fourier series for on
.
Note: Fourier series exists for every Riemann integrable function. But that series may or may not converge to .
Theorem 3.2:
If be bounded, integrable and monotone on
then
Proof. (i) Since is monotone on
, applying second mean value theorem (Weierstrass form) of integral calculus, there exists a
such that
Since 
Since 
Hence
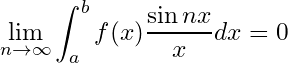
.
Proof: – (ii) For the integra 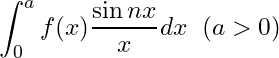
We write .
Since is bounded and monotone on
,
is also bounded and monotone on
for
and
.
By the second mean value theorem,
Since 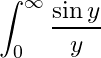
such that
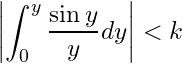
.
Therefore 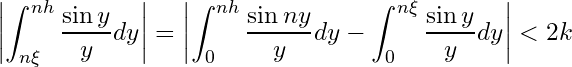
Since , for any positive
there exists a positive
such that
whenever
.
Hence 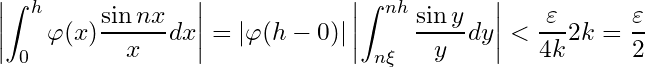
by
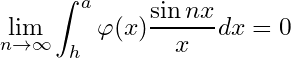
Hence of , there exists
such that
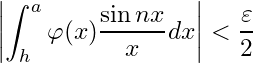
This implies
\ben*}
\left\vert\int_{0}^{a}\varphi(x)\dfrac{\sin nx}{x}dx\right\vert & \leq\left\vert\int_{0}^{h}\varphi(x)\dfrac{\sin nx}{x}dx\right\vert+\left\vert\int_{h}^{a}\varphi(x)\dfrac{\sin nx}{x}dx\right\vert\\
& <\dfrac{\varepsilon}{2}+\dfrac{\varepsilon}{2}=\varepsilon\text{ when and
.}
\end{align*}
Thus
Corollary 1. If is bounded integrable and monotone on
where
,
then
Proof. 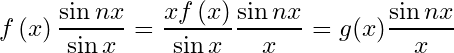
is bounded and integrable on
.
is monotone increasing on
and hence on
where
.
Then by Theorem 3.2
Corollary 2. If be bounded and integrable and monotone on
for
then
Proof. From (ii) of Theorem 3.2,
Since we have
Remark: the integrals in Theorem 3.2 are known as Dirichlet’s Integrals.
Theorem 3.3
If be bounded, integrable and monotone on
and
(not necessarily in the same sense), where
, then
where stand for Fourier coefficients of
.
Proof. From definition of we have
Theorem 3.4 (Fourier-Dirichlet):
If is bounded, integrable, periodic pf period
and it is piecewise monotone on
then the Fourier series for
in
is equal to
at
in
, when
is continuous at
,
![Rendered by QuickLaTeX.com \dfrac{\bm{1}}{\bm{2}}[f(x+0)+f(x-0)]}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-93d647a985d828f45e588a2283b1fa67_l3.png)
in
, when
and
exist,
![Rendered by QuickLaTeX.com \dfrac{\bm{1}}{\bm{2}}[f(\pi-0)+f(-\pi+0)]}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-ae9d308a6dbe16d4528ac7945424a4c6_l3.png)
, when
and
exist.
Proof. The Fourier series for (since it satisfies Dirichlet’s condition in
) in
is
where
and
Let,
Then
In the first integral, we will put and in the second integral, we are going to put
.
Then
Since satisfies Dirichlet’s conditions in
, if we consider
as functions of
then they satisfy Dirichlet’s conditions in
and in
respectively. If
exist then
and
have the limits when
tends to zero.
Hence, if , we have using Dirichlet’s integrals,
Hence (ii) proved.
If is continuous at
where
then
.
Hence,
which proves (i).
At ,
If and
exist, using Dirichlet’s integrals,
We have,
Similarly, it can be shown that
Remark: The Theorem 3.4 establishes the point-wise convergence of the Fourier series for to the function
and not the uniform convergence. The Fourier series expression of a function is unique.
Theorem 3.5. (Parseval’s Identity):
If the Fourier series for in
converges uniformly to
on
then
Where are the Fourier coefficients for
in
.
Proof. The Fourier series of in
is
Where
Since the series (1) converges uniformly to on
, then we can write (1) as
Multiplying both sides of (2) by and then integrating term-by-term (which is valid, since
is bounded on
or if
unbounded,
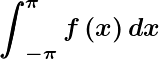
we have
Theorem 3.6. (Bessel’s Inequality)
If is bounded and integrable on
or if
is unbounded on
but
![Rendered by QuickLaTeX.com \bm{\int_{-\pi}^{\pi}{\left[f(x)\right]^2dx}}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-6857ae0ffb149480457a84ca9638e73d_l3.png)
Where are the Fourier coefficients for
in
.
Proof. The Fourier series expression for on
is
Where are given by
for all .
Let
Since ![Rendered by QuickLaTeX.com \int_{-\pi}^{\pi}{\left[f\left(x\right)-S_m\left(x\right)\right]^2dx\geq0}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e92e8abc7b994a3e4eaa557116894a17_l3.png)
From (1)
Again from (1),
Hence using (2), (3) and (4) we have the inequality
Note: Taking in Bessel’s inequality we obtain
Since and hence
is integrable on
, the series
SOME EXAMPLES ON FOURIER SERIES REPRESENTATION OF FUNCTIONS IN ![Rendered by QuickLaTeX.com \left[-\pi,\ \pi\right]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%2080%2026'%3E%3C/svg%3E)
Example 4.1. We are going to solve the Fourier series representation of in
where
and hence we will deduce that 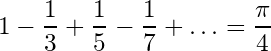
Solution: is continuous on
and hence it is bounded and integrable on
. Since
for
,
is monotone increasing on
. Thus
satisfies Dirichlet’s conditions on
so that
can be represented by a Fourier series
Hence the Fourier series expansion for in
is
Since is continuous on
, so we can write
Example 4.2. We are going to find the Fourier series expansion of the function
Hence we will deduce that
Solution: Since is an even function, its derivative
is odd and hence
is symmetric about origin.
in
and
. Hence
is piecewise monotone in
. Hence
satisfies Dirichlet’s conditions in
. Therefore
can be represented by the Fourier series
For 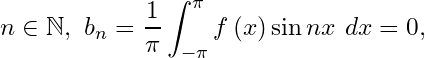
is an odd function.
Hence, Fourier series corresponding to in
is
Since is continuous on
,
Example 4.3. Obtain the Fourier series expansion of in
, where
Then we are going to show that the sum of the series
Solution: is piecewise monotone on
.
is continuous on
and hence is integrable on
. Thus
satisfies Dirichlet’s conditions in
.
So, can be represented by the Fourier series
where
For
Thus, the Fourier series expansion of in
is
i.e.,
Since is continuous on
,
Therefore,
Observation. If a function is not defined at
then
can be defined arbitrarily at those points. However, it is preferable to define
at those points in such a way that makes
continuous on
.
Example 4.4. We will find Fourier series of the periodic function with period
defined as
Then we will calculate the sum of the series at .
And we will prove that 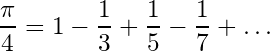
Solution: For the sake of continuity, we define
is piecewise monotone in
. It is bounded and periodic with period
.
is continuous on
except at
. Hence
is integrable on
. Thus
satisfies Dirichlet’s conditions on
. Hence
can be represented by Fourier series, which is
Where
Thus, Fourier series for in
is
At , the Fourier series for
converges to
Hence sum of the series at is
.
Since is continuous at
, we have
Example 4.5. If on
, we will prove that the Fourier series of
is given by
Then we will deduce that
and
Solution: is piecewise monotone on
.
is continuous on
and hence is integrable on
. Therefore
satisfies Dirichlet’s conditions on
. Hence
can be represented by Fourier series in
which is
where
Since is odd function, for
Hence the Fourier series for in
is
Since is continuous on
, we can write
Hence therefore,
Since
and
hence by Weierstrass M-test,
The 5series
[Remark: We can use comparison test for the test of convergence]
This implies the infinite series
converges uniformly to in
. Then by Parseval’s Identity (Theorem 3.5)
Example 4.6. Find the Fourier series of the periodic function with period
defined by
The we will find the sum of the series at and then we are going to show that
Solution: We define at
and at
as
, to make
continuous at
is piecewise monotone on
. It is continuous on
except at
and
and is bounded on
. Hence
is a bounded periodic and integrable function on
which validates the expansion of
into Fourier series, which is
Where
Thus, the Fourier series for in
is
i.e.
Since is periodic function of period
, so
. Since
is not continuous at
, the Fourier series for
converges at
![Rendered by QuickLaTeX.com \bm{x=4\pi+a \text{ to }\ \frac{1}{2}\left[f\left(a+0\right)+f\left(a-0\right)\right]=\frac{1}{2}}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-af29f9daad41c4e41f3d17cc76957095_l3.png)
Hence sum of the series at is equal to
.
At , the Fourier series for
converges to
Therefore
Example 4.7. Let be defined as follows:
We are going to obtain the Fourier’s coefficients and the Fourier series for the function and hence we will find that sum of the series can be represented as
Solution: is piecewise monotone in
. It is periodic with period
. It is bounded on
.
is continuous in
except at
. Hence it is integrable on
. Thus
satisfies Dirichlet’s conditions on
which validates Fourier series expansion of
in
.
The Fourier coefficients are
For ,
when is odd,
. When
is even,
For ,
Thus, we have
and
Hence the Fourier series for in
is
Since is continuous at
, the sum of the series at
is
Therefore,
FOURIER SERIES FOR EVEN AND ODD FUNCTIONS
When is an even function on
Then Fourier coefficients becomes zero, since
is then odd and hence
Thus the Fourier series for becomes a cosine series.
If is odd i.e.,
then the Fourier coefficients
and
Thus, the Fourier series for will be a sine series.
Example 5.1. We are going to consider the even function on
and we will see that it has a cosine series in Fourier’s form which is
Also the series converges to in
and by using this series we will show that,
Solution:
is piecewise monotone on
.
is bounded on
.
is continuous on
and hence is integrable on
. Thus
satisfies Dirichlet’s conditions on
and it can be represented by Fourier series on
, which is
Where
For
Hence
Since is odd function,
.
Thus, Fourier series for is in form of the cosine series
Since is continuous on
, so the series converges to
for all
and
We have
At , the sum of the series is
Therefore,
Example: 5.2. We will discuss for the odd function
has a sine series in Fourier’s form as
Then we will show that
[NOTE:- sinhx, coshx are hyperbolic functions.]
Solution: is an odd function on
and
is monotone increasing on
; it is bounded and integrable on
. Thus
satisfies Dirichlet’s conditions for expansion in Fourier series on
which will be a sine series as
Where
Hence Fourier series, which is a sine series, for on
is
Since is continuous on
, the series converges to
on
and we have for
At , the sum of the series is
Hence, we have
FOURIER EXPANSION ON ![Rendered by QuickLaTeX.com [0, \pi]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%2049%2026'%3E%3C/svg%3E) .
.
We have seen that satisfies Dirichlet’s conditions then
can be expressed either as a cosine series or as a sine series or as a combination of sine series and cosine series. If
is defined on
and it is bounded, integrable and piecewise monotone in
, then
can be extended over to
as a bounded, integrable and piecewise monotone even or odd function as desired and hence this function can be expressed as Fourier sine or cosine as desired.
Theorem 6.1.
If is periodic, bounded, integrable and piecewise monotone on
, then
Fourier cosine series of on
is
where
and
if
Fourier sine series of on
is
Where
And
Proof. (i) We define a function on
by
Then for all
and so
is an even function on
. Since
satisfies Dirichlet’s conditions on
,
also satisfies Dirichlet’s conditions on
, hence we have a Fourier cosine series (by Fourier-Dirichlet theorem)
Where
And
Also
(ii) We define a function on
by
Then i.e.,
is an odd function on
. Since
satisfies Dirichlet’s conditions on
,
also satisfies Dirichlet’s conditions on
.
Then we have a Fourier sine series
where
and
Hence the theorem proved.
Let we discuss some examples regarding with the theorem 6.1
Example 6.1. We are going to show that for
Then we will deduce that
Solution:
We are to represent in Fourier sine series in
. Since
satisfies Dirichlet’s conditions on
, the Fourier sine series (by Theorem 6.1.) for
on
is
where
being continuous on
, we have
The series
as
and
is a convergent series, hence by Weierstrass M-test, the series
is uniformly convergent and this series is the derivative of the series
Since
Hence using term-by-term differentiation (which is permissible) of the sine series in , we have
Example 6.2. Using the expansions of the functions and
in the interval
in cosines of multiple of
, we are going to prove the equality
Solution:
satisfies Dirichlet’s conditions in . The cosine series for
on
is
Where
As is continuous on
, we have
Let, satisfies Dirichlet’s conditions in
. The cosine series for
on
is
Where
And
As is continuous on
, we have
From (1),
From (2),
Therefore, adding these two convergent series in we have
Example 6.3. Show that the following function satisfies Dirichlet’s conditions of convergence of Fourier series in
:
,
Find a series of cosines of multiples of which is the Fourier expansion of
in
. Deduce that
Solution: is piecewise monotone on
, it is bounded on
. Except at
and
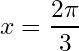
is continuous on
, and hence is Riemann integrable on
. Hence
satisfies Dirichlet’s conditions of convergence of Fourier series in
.
Fourier cosine series of in
is
where
which is non-zero when is odd but not multiple of 3.
Thus, cosine series for in
is
i.e.,
i.e.,
Since this series converges to at
So
Example 6.4. We are going to expand the function in a Fourier cosine series, where
is not an integer.
Solution: Let
is continuous and piecewise monotone on
. So,
satisfies Dirichlet’s conditions on
. Then Fourier cosine series of
on
is
Where,
And
Hence the Fourier cosine series of is
Example 6.5. We are going to express the function
in a Fourier series in .Then we will show that
Solution: is continuous, integrable, monotone on
. Thus,
satisfies Dirichlet’s conditions on
and Fourier series for
on
is
Where
For ,
For
Thus, Fourier series for on
is
i.e.,
Since this series converges to at
, hence
Hence we got our desired result.
SOME PROBLEMS FOR THE READERS
- Find the Fourier series for the function
- Find the Fourier series for the function
. And calculate the sum at
.
BIBLIOGRAPHY:
- Fourier Series, Transforms, and Boundary Value Problems
Book by J. Ray Hanna and John H. Rowland - Fourier series
Book by G. P. Tolstov - Fourier Series
Book by Rajendra Bhatia (Best book for Beginners) - Discourse on Fourier series
Book by Cornelius Lanczos
Thank you for reading the article we will meet in the next article……
Also, you may want to check our blog posts about Riemann Integral, Lebesgue Outer Measure, and All The Logarithm Rules You Know and Don’t Know About
And don’t forget to join us on our Facebook page stay updated on any new articles and a lot more!!!!!

![Rendered by QuickLaTeX.com \[\dfrac{1}{2}a_{0}+\sum_{n=1}^{\infty}(a_{n}\cos nx+b_{n}\sin nx)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8449e2045cfa64681dd6ed8e0efbe41c_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} f(x) & = 1-x, \;\;\; x\in \left[0,\dfrac{1}{2}\right]\\ & =x, \;\;\;\;\;\;\;\;\; x\in \left[\dfrac{1}{2},1\right] \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-391b8f9fa42dbc92c31a0cead9eba993_l3.png)
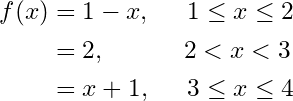
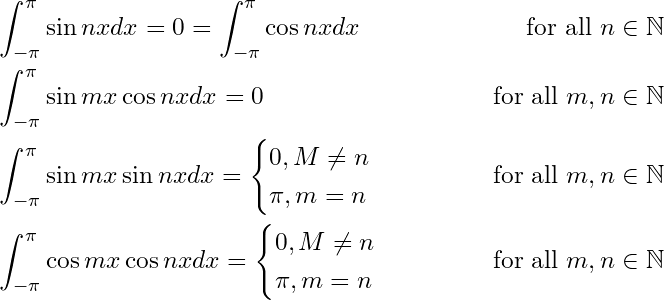
![Rendered by QuickLaTeX.com \[\dfrac{1}{2}a_{0}\sum_{n=1}^{\infty}(a_{n}\cos nx+b_{n}\sin nx)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-187e0ed7715cb9e0460dfa9e16110e86_l3.png)
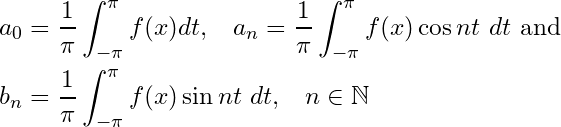
![Rendered by QuickLaTeX.com \[\int_{a}^{b}f_{m}(x)f_{n}(x)dx=0 \text{ for } m\neq n\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5f4f5b456cee83ecedcbbd3102869446_l3.png)
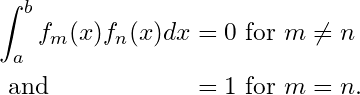
![Rendered by QuickLaTeX.com \begin{equation*} f(x)=\dfrac{1}{2}a_{0}\sum_{n=1}^{\infty}(a_{n}\cos nx+b_{n}\sin nx), x\in[-\pi,\pi] \end{equation*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-6dc327ff86ec60d239bf6fb6e2f62e06_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \int_{-\pi}^{\pi}f(x)dx & =\dfrac{1}{2}a_{0}\int_{-\pi}^{\pi} dx + \sum_{n=1}^{\infty}\left[ a_{n} \int_{-\pi}^{\pi}\cos nx\ dx + b_{n}\int_{-\pi}^{\pi}\sin nx\ dx \right]\\ & =a_{0}\pi\\ \Rightarrow a_{0}& = \dfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-678c89512419a634b18d3c41c76a6b92_l3.png)
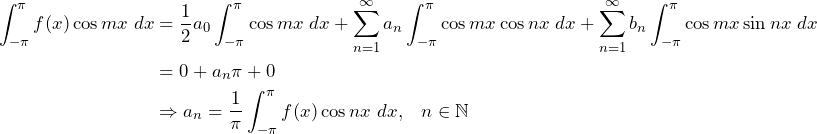
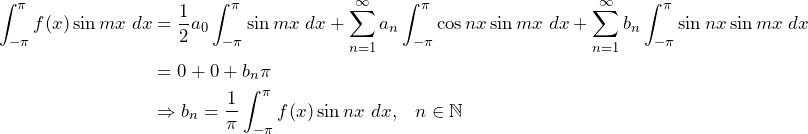
![Rendered by QuickLaTeX.com \begin{align*} &\lim_{n\to\infty}\int_{a}^{b}f(x)\dfrac{\sin nx}{x}dx =0 \text{ and}\\ &\lim_{n\to\infty}\int_{0}^{a}f(x)\dfrac{\sin nx}{x}dx =\dfrac{\pi}{2}f(0+), \text{ if } f:[0,a]\to\mathbb{R} \text{ is bounded and integrable on } [0,a]\\ &\text{ and is monotone on } [0,h] \text{ for } 0<h<a. \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-fde0ae3510db1331681ae9d9d0c63e27_l3.png)
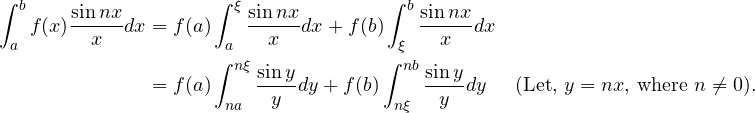
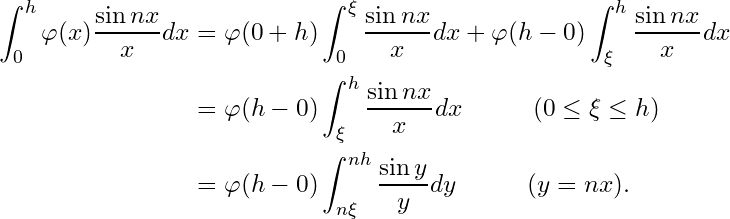
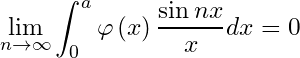
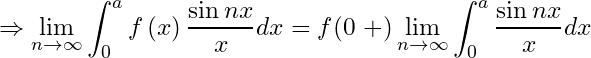
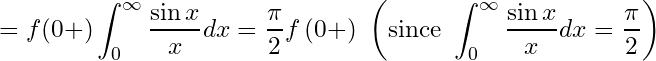
![Rendered by QuickLaTeX.com \[\displaystyle\lim_{n\rightarrow\infty}{\int_{a}^{b}{f\left(x\right)\frac{\sin{nx}}{\sin{x}}dx=0\ \left(0<a<b<\frac{\pi}{2}\right)}}.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-742cd7e00d71289460ce69703c233179_l3.png)
![Rendered by QuickLaTeX.com \[\displaystyle\lim_{n\rightarrow\infty}{\int_{a}^{b}{g\left(x\right)\frac{\sin{nx}}{x}dx=0}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e61b39f313d721e9a3ef1d36d56b7835_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow\lim_{n\rightarrow\infty}{\int_{a}^{b}{f\left(x\right)\frac{\sin{nx}}{\sin{x}}dx=0\ \ \left(0<a<b<\frac{\pi}{2}\right)}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d7cf03c9d7c4c17b0e2734e86107cd2b_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}{\int_{0}^{a}{f\left(x\right)\frac{\sin{nx}}{\sin{x}}dx=\frac{\pi}{2}f\left(0+\right).}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2f34891807ad0b79872371f51b199c26_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}{\int_{0}^{a}{g(x)\frac{\sin{nx}}{x}dx}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-6f14602bdff45bf96a52be0ba8017b32_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}{\int_{0}^{a}{f\left(x\right)\frac{\sin{nx}}{\sin{x}}dx=\frac{\pi}{2}}}f\left(0+h\right)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-fea8fbb36683df78334dcf7547e153d3_l3.png)
![Rendered by QuickLaTeX.com \[\dfrac{1}{2}a_{0}+\sum_{n=1}^{\infty}a_{n}=\dfrac{1}{2}\left[f(0+)+f(0-)\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-dc5deee41c46c07fe4a297c31eb9c9fc_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \frac{1}{2}a_0+\sum_{n=1}^{k}{a_n & =\frac{1}{2\pi}}\int_{-\pi}^{\pi}{f\left(x\right)dx+\sum_{n=1}^{k}\frac{1}{\pi}}\int_{-\pi}^{\pi}{f\left(x\right)\cos{nx\ dx}}\\ & =\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left(x\right)dx+\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)\sum_{n=1}^{k}\cos{nx\ dx}}}\\ & =\frac{1}{2\pi}\int_{-\pi}^{\pi}{f(x)\left[1+2\frac{\sin{\left(\frac{kx}{2}\right)}}{\sin{\frac{x}{2}}}\cos{(k+1)\frac{x}{2}}\right]dx}\\ & =\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left(x\right)\ \left[1+\frac{\sin{\left(k+\frac{1}{2}\right)x-\sin{\frac{x}{2}}}}{\sin{\frac{x}{2}}}\right]dx}\\ & =\frac{1}{2\pi}\int_{-\pi}^{0}{f\left(x\right)\ \frac{\sin{\left(k+\frac{1}{2}\right)x}}{\sin{\frac{x}{2}}}}dx+\frac{1}{2\pi}\int_{0}^{\pi}{f(x)\frac{\sin{\left(k+\frac{1}{2}\right)x}}{\sin{\frac{x}{2}}}dx}\\ & =\frac{1}{\pi}\int_{-\frac{\pi}{2}}^{0}{f\left(-2y\right)\frac{\sin{\left(2k+1\right)y}}{\sin{y}}dy+\frac{1}{\pi}\int_{0}^{\frac{\pi}{2}}{f\left(2y\right)\frac{\sin{\left(2k+1\right)y}}{\sin{y}}dy\ (\text{ Putting }\ x=2y)}}\\ & \text{Now taking } limit\ k\rightarrow\infty \text{ we have }\\ \frac{1}{2}a_0+\sum_{n=1}^{\infty}{a_n & =\frac{1}{\pi}}\left[f\left(0-\right)+f\left(0\ +\right)\right]\frac{\pi}{2}\ (\text{From\ Corollary}\ 2.)\\ & =\frac{1}{2}\left[f\left(0+\right)+f(0\ -)\right]. \text{(Hence Proved)} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1f1768cf77f28801d4833982fbe90bac_l3.png)
![Rendered by QuickLaTeX.com \[f(x)\sim\frac{1}{2}a_{0}+\sum_{n=1}^{\infty}{\left(a_{n}\cos{nx}+b_{n}\sin{nx}\right),}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-284c15165d26d3f672175c0d7786f443_l3.png)
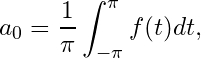
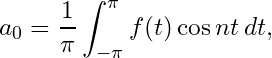
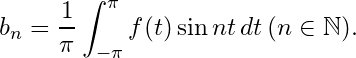
![Rendered by QuickLaTeX.com \[S_{n}(x)=\frac{1}{2}a_{0}+\sum_{m=1}^{n}{\left(a_{m}\cos{mx}+b_{m}\sin{mx}\right),} \, n\in\mathbb{N}.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e22ba85938afea6a2b0deeac1d7603bd_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} S_n\left(x\right) & =\frac{1}{2\pi}\int_{-\pi}^{\pi}{f(t)\left[1+\sum_{m=1}^{n}{(2\cos{mt\cos{mx+2\sin{mt\sin{mx)}}}}}\right]}dt\\ & =\frac{1}{2\pi}\int_{-\pi}^{\pi}{f(t)\left[1+2\sum_{m=1}^{n}\cos{m(t-x)}\right]}dt\\ & =\frac{1}{2\pi}\int_{-\pi}^{\pi}{f(t)\left[1+2\frac{\sin{\frac{n(t-x)}{2}}}{\sin{\frac{t-x}{2}}}\cos{\frac{(n+1)(t-x)}{2}}\right]dt}\\ & =\frac{1}{2\pi}\int_{-\pi}^{\pi}{f(t)\frac{\sin{\left(\frac{2n+1}{2}\left(t-x\right)\right)}}{\sin{\left(\frac{t-x}{2}\right)}}dt}\\ & =\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left(t\right)\frac{\sin{\frac{1}{2}\left(2n+1\right)\left(t-x\right)}}{\sin{\frac{1}{2}}\left(t-x\right)}dt+\frac{1}{2\pi}\int_{x}^{\pi}{f\left(t\right)\frac{\sin{\frac{1}{2}\left(2n+1\right)\left(t-x\right)}}{\sin{\frac{1}{2}}\left(t-x\right)}dt.}} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-7d1c0c6f48203b5e5123833c9db4f786_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \lim_{n\rightarrow\infty}S_n\left(x\right) &=\frac{1}{\pi}\left[f\left(x-0\right)\frac{\pi}{2}+f(x+0)\frac{\pi}{2}\right]\\ & =\frac{1}{2}\left[f\left(x-0\right)+f(x+0)\right] \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9606164520e6a2956a1caee1cb3e7eec_l3.png)
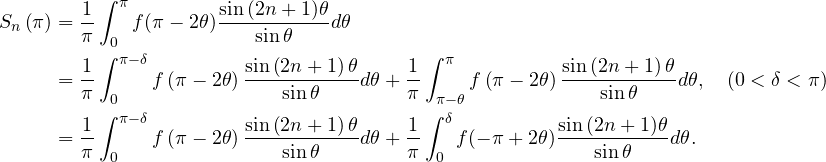
![Rendered by QuickLaTeX.com \begin{align*} \lim_{n\rightarrow\infty}S_n\left(\pi\right) & =\frac{1}{\pi}f\left(\pi-0\right)\frac{\pi}{2}+\frac{1}{\pi}f(-\pi+0)\frac{\pi}{2}\\ & =\frac{1}{2}\left[f\left(-\pi+0\right)+f(\pi-0)\right]. \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-a848eb905ffdbd1a88485fa04d0df3c9_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}S_n\left(-\pi\right)=\frac{1}{2}\left[f\left(-\pi+0\right)+f(\pi-0)\right], \text{ \textbf{which proves (iii)} }\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-472c42c48a93779d66abec2c39859994_l3.png)
![Rendered by QuickLaTeX.com \[\bm{\frac{1}{2}}\bm{a_0^2+\sum_{n=1}^{\infty}(a_{0}^{2}+b_{n}^{2})=}\bm{\frac{1}{\pi}\int_{-\pi}^{\pi}[fx]^{2}dx}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-6e75aebeeaef1244b532207f83e2f500_l3.png)
![Rendered by QuickLaTeX.com \[f(x)~\frac{1}{2}a_0+\sum_{n=1}^{\infty}{(a_n\cos{nx+b_n\sin{nx)}}}\ldots\ (1)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-cf3d647169812a068f49c7174db25111_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)=\frac{1}{2}a_0+\sum_{n=1}^{\infty}{(a_n\cos{nx}+b_n\sin{nx)}}, \ \ x\in[-\pi,\pi]\ldots\ (2).\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b7129e3d79fcb584c489d90e97466293_l3.png)
![Rendered by QuickLaTeX.com \[\int_{-\pi}^{\pi}{\left[f\left(x\right)\right]^2dx=\frac{1}{2}a_0\int_{-\pi}^{\pi}{f\left(x\right)dx+\sum_{n=1}^{\infty}\left[a_n\int_{-\pi}^{\pi}{f\left(x\right)\cos{nx\ dx+b_n\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx}}}}\right]}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-eba4f6be0f983b0632b8841f8f73b8b3_l3.png)
![Rendered by QuickLaTeX.com \[\int_{-\pi}^{\pi}{\left[f\left(x\right)\right]^2dx}=\frac{\pi}{2}a_0^2+\pi\sum_{n=1}^{\infty}\left(a_n^2+b_n^2\right).\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-f0588fad577fe9377a9fb07f507a5dc7_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow\frac{1}{2}a_0^2+\sum_{n=1}^{\infty}{\left(a_n^2+b_n^2\right)=\frac{1}{\pi}\int_{-\pi}^{\pi}{\left[f(x)\right]^2dx.}} \text{ \textbf{(Hence\ Proved)}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1231146dad20ae8931e724a17bed6104_l3.png)
![Rendered by QuickLaTeX.com \[\bm{\frac{1}{2}a_0^2+\sum_{n=1}^{m}\left(a_n^2+b_n^2\right)}\bm{\leq}\bm{\frac{1}{\pi}\int_{-\pi}^{\pi}\left[f\left(x\right)\right]^{2}dx, \ (m\in\mathbb{N})}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-04e1c9aa28d91d22f60c6f90d7e8e9c2_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}a_0+\sum_{n=1}^{\infty}{(a_n\cos{nx+b_n\sin{nx)}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-68f0882cba50660bdce862c6fc286668_l3.png)
![Rendered by QuickLaTeX.com \[S_m\left(x\right)=\frac{1}{2}a_0+\sum_{n=1}^{m}{(a_n\cos{nx+b_n\sin{nx),\ \ \ \left(m\in\mathbb{N}\right)\ldots\left(1\right).}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-229fe67f624676890020267fc4c8a9ac_l3.png)
![Rendered by QuickLaTeX.com \[2\int_{-\pi}^{\pi}{f\left(x\right)S_m\left(x\right)dx-\int_{-\pi}^{\pi}{\left[S_m(x)\right]^2dx\le\int_{-\pi}^{\pi}{\left[f(x)\right]^2dx\ldots\left(2\right).}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5e0735225b788527134b315cea5a8166_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \int_{-\pi}^{\pi}S_m\left(x\right)\ f\left(x\right)dx & =\frac{1}{2}a_0\int_{-\pi}^{\pi}f\left(x\right)dx\\ & +\sum_{n=1}^{m}\left[a_n\int_{-\pi}^{\pi}{f\left(x\right)\cos{nx\ dx+b_n\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx}}}}\right]\\ \Rightarrow\int_{-\pi}^{\pi}S_m\left(x\right)f\left(x\right)dx & =\pi\left[\frac{1}{2}a_0^2+\sum_{n=1}^{m}\left(a_n^2+b_n^2\right)\right]\ldots\left(3\right). \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c0303586f0e8642c70a7f4bca42c1cad_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \int_{-\pi}^{\pi}\left[S_m(x)\right]^2dx & =\frac{1}{4}a_0^2\int_{-\pi}^{\pi}dx+a_0\left[\sum_{n=1}^{\infty}{a_n\int_{-\pi}^{\pi}\cos{nx\ dx+b_n\int_{-\pi}^{\pi}\sin{nx\ dx}}}\right]\\ & +\int_{-\pi}^{\pi}{\left\{\sum_{n=1}^{m}\left(a_n\cos{nx+b_n\sin{nx}}\right)\right\}^2dx}\\ & =\pi\left[\frac{1}{2}a_0^2+\sum_{n=1}^{m}{(a_n^2+b_n^2)}\right]\ldots(4) \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-673f8ef6177f5ece5a4ada6d2af20d4d_l3.png)
![Rendered by QuickLaTeX.com \[\left(\because\int_{-\pi}^{\pi}{{cos}^2nx\ dx=\pi=\int_{-\pi}^{\pi}{{sin}^2nx\ dx}}\ and\ \int_{-\pi}^{\pi}\cos{nx\sin{nx\ dx=0,\ \ \ n\in\mathbb{N}}}\right).\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8a3f9d098bd314374702a90bf6de1da3_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}a_0^2+\sum_{n=1}^{m}{\left(a_n^2+b_n^2\right)\le\frac{1}{\pi}\int_{-\pi}^{\pi}{\left[f\left(x\right)\right]^2dx}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-319c05edde98eb9bacb17c58a1bdac30_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}a_0^2+\sum_{n=1}^{\infty}{\left(a_n^2+b_n^2\right)\le\frac{1}{\pi}\int_{-\pi}^{\pi}{\left[f\left(x\right)\right]^2dx.}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-96c829bdf5f325d865e7a6e2c32901a3_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{\left(a_n^2+b_n^2\right)\text{ is\ convergent.}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5e02c60b12793ca69080a8029532c3a9_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \text{ Where}, a_0 & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)dx=0 (\because f \text{ is odd})}\\ a_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\cos{nx}dx,\ \left(n\in\mathbb{N}\right)=0} \text{ (Since f is odd and hence $f(x)\cos\ nx$ is odd for all $n\in\mathbb{N}$)}\\ b_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx,\ \ \ (n\in\mathbb{N})}}\\ & =\frac{2}{\pi}\int_{0}^{\pi}{x\sin{nx\ dx}}\\ & =\frac{2}{\pi}\left\{\left[-\frac{x}{n}\cos{nx}\right]_0^\pi+\frac{1}{n}\int_{0}^{\pi}\cos{nx\ dx}\right\}\\ & =-\frac{2}{n}\cos{n\pi}\\ & ={(-1)}^n\frac{2}{n}. \text{ According as n is even or odd. [Since,$\cos nx={(-1)}^n$]} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-cdb421e84685b59a76f32c88ae894a8f_l3.png)
![Rendered by QuickLaTeX.com \[=\sum_{n=1}^{\infty}{b_n\sin{nx=2\left[\frac{\sin{x}}{1}-\frac{\sin{2x}}{2}+\frac{\sin{3x}}{3}-\ldots\right]}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-7aacdbd0ee2b098c881aa4f8b42918b7_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)=2\left[\frac{\sin{x}}{1}-\frac{\sin{2x}}{2}+\frac{\sin{3x}}{3}-\frac{\sin{4x}}{4}+\ldots\right],\ \ x\in\left[-\pi,\ \pi\right].\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-4c976e311ccff10ca4e513ce6414eadb_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \text{ At } x & =\frac{\pi}{2}\in\left[-\pi,\ \pi\right],\\ \frac{\pi}{2} & =2\left[1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\ldots\right]\\ \Rightarrow & 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\ldots=\frac{\pi}{4}. \text{\textbf{(Hence we got our desire result.)}} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-73def1431c438a83973de4eccddc32fd_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\pi}{4}=\frac{1}{2}+\frac{1}{1\cdot3}-\frac{1}{3\cdot5}+\frac{1}{5\cdot7}-\ldots\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2e65adcc264f2e570ad2da593429f8ff_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}a_0+\sum_{n=1}^{\infty}{(a_n\cos{nx+}b_n\sin{nx)}.}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d711f0e89a3fbca6fd266148184b9626_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \text{Where } a_0 & =\frac{1}{\pi}\int_{-\pi}^{\pi}f\left(x\right)dx =\frac{2}{\pi}\ \int_{0}^{\pi}{x\sin{x\ dx}}\\ & =\frac{2}{\pi}\left\lbrace-x\cos x]_{0}^{\pi}+\int_{0}^{\pi}\cos x\,dx\right\rbrace=\frac{2}{\pi}\cdot\pi=2; \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e357f60b4bbed20e4fe5fd5ad891d40d_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \text{For } n\in N,\ \ \bm{a_n} & \bm{=\frac{1}{\pi}\int_{-\pi}^{\pi}f\left(x\right)\cdot\cos{nx}dx=\frac{2}{\pi}\ \int_{0}^{\pi}{x\sin{x\cos{nx}dx}}}\bm{\left[}\textbf{\text{ even function }}\bm{\right]}\\ & =\frac{1}{\pi}\int_{0}^{\pi}x\left(\sin{\left(n+1\right)}x-\sin{\left(n-1\right)}x\right)dx \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-fbd97ecb93ba088aa484a215e29be52d_l3.png)
![Rendered by QuickLaTeX.com [\text{Since },2\cos{\left(\frac{A+B}{2}\right)}\sin{\left(\frac{A-B}{2}\right)}=sinA-sinB]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-53548de4112c44ae31ccf0c70f419482_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \text{For } n>1,\ \ a_n & =\frac{1}{\pi}\left\{\left[x\cdot\frac{\cos{\left(n-1\right)x}}{n-1}-x\cdot\frac{\cos{\left(n+1\right)}x}{n+1}\right]_0^\pi+\int_{0}^{\pi}\left[\frac{\cos{\left(n+1\right)}x}{n+1}-\frac{\cos{\left(n-1\right)}x}{n-1}\right]dx\right\}\\ & ={(-1)}^{n-1}\left[\frac{1}{n-1}-\frac{1}{n+1}\right]={(-1)}^{n-1}\frac{2}{n^2-1} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9c5eaabddee6eee7fe035404bca26ab1_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \text{When } n=1,\ a_1 & =\frac{1}{\pi}\int_{0}^{\pi}{x\sin{2x\ dx=\frac{1}{\pi}\left\{\left[\frac{-x\cos{2x}}{2}\right]_0^\pi+\frac{1}{2}\int_{0}^{\pi}\cos{2xdx}\right\}}}\\ & =-\frac{1}{2}. \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-381c8a29a0b67618a5bdf9879a60bd6d_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)\sim\ 1-\frac{1}{2}\cos{x+2\sum_{n=2}^{\infty}{\frac{{(-1)}^{n-1}}{n^2-1}\cos{nx.}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-a44b4baae970c75aa6e3e3d7e980a609_l3.png)
![Rendered by QuickLaTeX.com \[f\left(\frac{\pi}{2}\right)=1-\frac{1}{2}\cos{\frac{\pi}{2}+}2\sum_{n=2}^{\infty}{\frac{{(-1)}^{n-1}}{n^2-1}\cos{\frac{n\pi}{2}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b6849ed2c033ca611f1e02e984d6b904_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow\frac{\pi}{2}=1+2\left[\frac{1}{2^2-1}-\frac{1}{4^2-1}+\frac{1}{6^2-1}-\ldots\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-47e71fa7406cf47dc27ab40a69fe95b3_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow\frac{\pi}{4}=\frac{1}{2}+\frac{1}{1\cdot3}-\frac{1}{3\cdot5}+\frac{1}{5\cdot7}-\ldots \textbf{\text{ (Hence we are done)}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-03f37aabf054aafaf3117b49bb5b6e11_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{\begin{matrix}0\ \ \ \ ,-\pi\le x<0\\\frac{1}{4}\pi x\ \ \ \ ,0\le x\le\pi\\\end{matrix}\right.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-0d59d90e0fc8fb40f93d84f05fdff56d_l3.png)
![Rendered by QuickLaTeX.com \[1+\frac{2}{3^2}+\frac{2}{5^2}+\ldots \text{ is equal to } \frac{\pi^2}{8}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c2ec7b31af6efd5350fe4a5470262c75_l3.png)
![Rendered by QuickLaTeX.com \[a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)dx=\frac{1}{4}\int_{0}^{\pi}{x\ dx=\frac{\pi^2}{8}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1cd76e471c8bf998cdda1861305b0ff9_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} n\in\mathbb{N},\ a_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\cos{nx\ dx=\frac{1}{4}\int_{0}^{\pi}{x\cos{nx\ dx}}}}\\ & =\frac{1}{4}\left\{\left[\frac{x\sin{nx}}{n}\right]_0^\pi-\frac{1}{n}\int_{0}^{\pi}\sin{nx\ dx}\right\}\\ & =\frac{1}{4n^2}(\cos{n\pi-1)=\frac{1}{4n^2}\left({(-1)}^n-1\right)} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-407ebd1d98ead8a0018b22c9f84e620e_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} b_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx=\frac{1}{4}\int_{0}^{\pi}{x\sin{nx\ dx}}}}\\ & =\frac{1}{4}\left\{\left[-\frac{1}{n}x\cos{nx}\right]_0^\pi+\frac{1}{n}\int_{0}^{\pi}\cos{nx\ dx}\right\}\\ & =-\frac{1}{4n}\pi\cos{n\pi=-\frac{\pi}{4n}{(-1)}^n} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-383c9eb41a07e47899f6812149622cce_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\pi^2}{16}+\frac{1}{4}\sum_{n=1}^{\infty}{\frac{1}{n^2}\left({(-1)}^n-1\right)\cos{nx-\frac{\pi}{4}\sum_{n=1}^{\infty}{\frac{1}{n}\left(-1\right)^n\sin{nx}}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9a325e92b458836d2ca57bf4c204e33b_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\pi^2}{16}-\frac{1}{2}\left[\frac{\cos{x}}{1^2}+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots\right]+\frac{\pi}{4}\left[\frac{\sin{x}}{1}-\frac{\sin{2x}}{2}+\frac{\sin{3x}}{3}-\ldots\right].\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-99267a4e72204ba0a63013017f167e2c_l3.png)
![Rendered by QuickLaTeX.com \[f\left(0\right)=\frac{\pi^2}{16}-\frac{1}{2}\left[\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+\ldots\right] \text{ and } f\left(0\right)=0.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-aee6b41af3313a55b61c997b3d9c758d_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+\ldots=\frac{\pi^2}{8}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9d73a594cf09f5126ea98cf7f93fe27b_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{\begin{matrix}-1,\ -\pi<x<0\\1\ \ ,\ \ \ 0\le x<\pi\\\end{matrix}\right.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-ca4e850e824b6cc7de7894b7ce0489c5_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}a_0+\sum_{n=1}^{\infty}{(a_n\cos{nx+b_n\sin{nx),}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-be47645345982a95863401ac9996daff_l3.png)
![Rendered by QuickLaTeX.com \[a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)dx}=0\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-bc671afe517f2458bd417d1bdc80989f_l3.png)
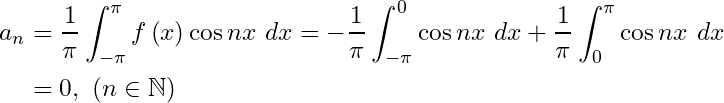
![Rendered by QuickLaTeX.com \begin{align*} b_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx=-\frac{1}{\pi}\int_{-\pi}^{0}{f\left(x\right)\sin{nx\ dx+\frac{1}{\pi}\int_{0}^{\pi}{f\left(x\right)\sin{nx\ dx}}}}}}\\ & =\frac{2}{n\pi}[1-\cos n\pi]=0 \text{ when $n$ is even}\\ & =\frac{4}{n\pi} \text{ when $n$ is odd.} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-608fcc973ee314c4183728f5632d8d9c_l3.png)
![Rendered by QuickLaTeX.com \[\frac{4}{\pi}\left[\frac{\sin{x}}{1}+\frac{\sin{3x}}{3}+\frac{\sin{5x}}{5}+\ldots\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-843ba1201c257b2eeb6c891b7b85edfc_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}[f\left(-\pi+0\right)+f\left(\pi-0\right)]=\frac{1}{2}\left[-1+1\right]=0\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-54c73d1564bae5cc4dd2d0d2e59fe431_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} f\left(\frac{\pi}{2}\right) & =\frac{4}{\pi}\left[\frac{\sin{\frac{\pi}{2}}}{1}+\frac{\sin{\frac{3\pi}{2}}}{3}+\frac{\sin{\frac{5\pi}{2}}}{5}+\frac{\sin{\frac{7\pi}{2}}}{7}+\ldots\right]\\ \Rightarrow\frac{\pi}{4} & =1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\ldots \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d6694aaab86c5a35faea39ebb87d15cc_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)=\frac{\pi^2}{3}+4\sum_{n=1}^{\infty}\frac{\cos{nx}}{n^2}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-f424e2d28309862418c95fcbd9f8989f_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{\frac{1}{n^2}=\frac{\pi^2}{6}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b17a295d051f2a1306ef2b54a8987162_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}\frac{1}{n^4}=\frac{\pi^4}{90}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5174d8dc2e1aa3f378c80cb820ad9ef9_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} a_0 & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)dx=\frac{2}{\pi}\int_{0}^{\pi}{\left(\pi-x\right)^2dx=\frac{2}{\pi}\left[\pi^3-\pi^3+\frac{\pi^3}{3}\right]=\frac{2}{3}\pi^2,}}\\ a_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\cos{nx}dx=\frac{2}{\pi}\int_{0}^{\pi}{\left(\pi-x\right)^2\cos{nx}dx}}\\ & =\frac{2}{\pi}\left[\pi^2\int_{0}^{\pi}\cos{nx\ dx-2\pi\int_{0}^{\pi}{x\cos{nx\ dx+\int_{0}^{\pi}{x^2\cos{nx\ dx}}}}}\right]\\ & =\frac{2}{\pi}\left[0-2\pi\left\{\left[\frac{x}{n}\sin{nx}\right]_0^\pi-\frac{1}{n}\int_{0}^{\pi}\sin{nx\ dx}\right\}+\left[\frac{x^2}{n}\sin{nx}\right]_0^\pi-\frac{2}{n}\int_{0}^{\pi}{x\sin{nx\ dx}}\right]\\ & =\frac{2}{\pi}\left[\frac{2\pi}{n^2}(1-\cos{n\pi)-\frac{2}{n}\left\{\left[-\frac{x}{n}\cos{nx}\right]_0^\pi+\frac{1}{n}\int_{0}^{\pi}\cos{nx\ dx}\right\}}\right]\\ & =\frac{2}{\pi}\left[\frac{2\pi}{n^2}(1-\cos{n\pi)+\frac{2\pi}{n^2}\cos{n\pi}}\right]\\ & =\frac{4}{n^2},\ \ (n\in\mathbb{N}) \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2594186b0840c685bfb414e3b83da242_l3.png)
![Rendered by QuickLaTeX.com \[b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx=0,}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-a49cb08ce3d9befdc664be2e595bcd5b_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{3}\pi^2+4\sum_{n=1}^{\infty}\frac{\cos{nx}}{n^2}\ \textbf{\text{(Proving the 1st part)}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-eade55653596331035852f67416b4e43_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} f\left(x\right) & =\frac{1}{3}\pi^2+4\sum_{n=1}^{\infty}{\frac{\cos{nx}}{n^2},\ \ \ x\in\left[-\pi,\ \pi\right]}\\ \Rightarrow f\left(0\right) & =\frac{1}{3}\pi^2+4\sum_{n=1}^{\infty}\frac{1}{n^2}\ \bm{\left(}\textbf{\text{Putting }} \bm{x=0\right)}\\ \Rightarrow\pi^2 & =\frac{1}{3}\pi^2+4\sum_{n=1}^{\infty}\frac{1}{n^2} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-a1b8532e684d20ea05cc349873f1e567_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow\sum_{n=1}^{\infty}{\frac{1}{n^2}=\frac{\pi^2}{6}}.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5d9a55b4927472362ba427f697ac5685_l3.png)
![Rendered by QuickLaTeX.com \[\left|\frac{\cos{nx}}{n^2}\right|\le\frac{1}{n^2},\ x\in\left[-\pi,\ \pi\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d7cc23b463373786efbb4bb5836f240a_l3.png)
![Rendered by QuickLaTeX.com \[\bm{\sum_{n=1}^{\infty}\frac{1}{n^2} \textbf{\text{ is a convergent series, ($P$ series where $p>1$)}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-699a1be432b4ab91d75b60842d84799f_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{\frac{\cos{nx}}{n^2}\text{ is uniformly convergent.}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8e01171648e0a91b2f55d357f9306285_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{3}\pi^2+4\sum_{n=1}^{\infty}\frac{\cos{nx}}{n^2}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8ecfdad6b08a1b736fbed497d8b87d15_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}a_0^2+\sum_{n=1}^{\infty}{(a_n^2{+b}_n^2)}=\frac{1}{\pi}\int_{-\pi}^{\pi}\left[f(x)\right]^{2} dx\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-09f001e310407bd10e64d0205ab96a81_l3.png)
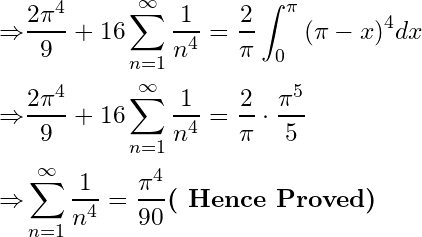
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{\begin{matrix}0,\ -\pi<x<a\\1,\ a\le x\le b\ \ \ \\0,\ b<x<\pi\ \ \ \\\end{matrix}\right.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1514c345f514e5a04cee5dc648769885_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{\frac{\sin{n(b-a)}}{n}=\frac{\pi-b+a}{2}.}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-f83fbe0c5029d31df6168c030d6ccc82_l3.png)
![Rendered by QuickLaTeX.com \[\text{Then } f\left(x\right)=\left\{\begin{matrix}0,\ -\pi\le x<a\\1,\ a\le x<b\ \ \ \\0,\ b\le x\le\pi\ \ \ \\\end{matrix}\right.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9dec91d76b8141765ae457aae7820abd_l3.png)
![Rendered by QuickLaTeX.com \[a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)dx=\frac{1}{\pi}\ \int_{a}^{b}{dx=\frac{1}{\pi}(b-a)}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-178346d5508a3e9dae18688d7feb65d9_l3.png)
![Rendered by QuickLaTeX.com \[a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx\ dx=\dfrac{1}{\pi}\int_{a}^{b}\cos{nx}\ dx=\dfrac{1}{n\pi}\left[\sin{nb}-\sin{na}\right], \ \ n\in\mathbb{N}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5da36aec849dd71dbc4c0c28405fd40f_l3.png)
![Rendered by QuickLaTeX.com \[b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx}\ dx=\frac{1}{\pi}\ \int_{a}^{b}{\sin{nx}\ dx=\frac{1}{n\pi}\left(\cos{na-\cos{nb}}\right),\ \ \ n\in\mathbb{N}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5efd94d411c61f7e22b31bb64c894d9a_l3.png)
![Rendered by QuickLaTeX.com \[\bm{\frac{1}{2\pi}\left(b-a\right)+\frac{1}{\pi}\sum_{n=1}^{\infty}{\frac{1}{n}\left[\cos{nx(\sin{nb-\sin{na)+\sin{nx(\cos{na-\cos{nb)}}}}}}\right]}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-aadb2ac2210dbd4ee27225907db1488e_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2\pi}\left(b-a\right)+\frac{1}{\pi}\sum_{n=1}^{\infty}{\frac{1}{n}\left[\sin{n\left(x-a\right)+\sin{n(b-x)}}\right]}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2eb146621d9e5dba6fe4959d406474f3_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}\left[f\left(b+0\right)+f\left(b-0\right)\right]=\frac{1}{2}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-4ff27d82192a1424a681d6341112e0de_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}=\frac{b-a}{2\pi}+\frac{1}{\pi}\sum_{n=1}^{\infty}\frac{\sin{n\left(b-a\right)}}{n}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c1fa4804e831a57ee8cf85b133d45bf1_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow\sum_{n=1}^{\infty}{\frac{\sin{n\left(b-a\right)}}{n}=\frac{\pi-b+a}{2}}\textbf{(Proved)}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d89c46856d0f03af17cdeee03006edb0_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{\begin{matrix}\cos{x,\ 0\le x\le\pi}\\-\cos{x,\ -\pi}\le x<0\\\end{matrix}\right.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-ad6fa921360b46a7408b36902096fac8_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2}{1\cdot3}-\frac{6}{5\cdot7}+\frac{10}{9\cdot11}-\ldots\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-11024c18eeeb7f9b850b7a0943df2aa6_l3.png)
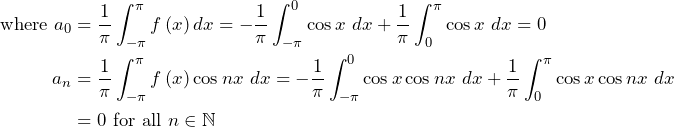
![Rendered by QuickLaTeX.com \begin{align*} b_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx=-\frac{1}{\pi}\int_{-\pi}^{0}\cos{x\sin{nx\ dx+\frac{1}{\pi}}}}}\int_{0}^{\pi}\cos{x\sin{nx\ dx}}\\ & =\frac{2}{\pi}\int_{0}^{\pi}\cos{x\sin{nx\ dx}}\\ & =\frac{1}{\pi} \left[\sin(n+1)x+\sin(n-1)x\right] dx,\ n\in\mathbb{N} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-4ead8572a3f036d084e501242ea124a5_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} b_n & =\frac{1}{\pi}\left[-\frac{\cos{\left(n+1\right)x}}{n+1}-\frac{\cos{\left(n-1\right)x}}{n-1}\right]_0^\pi\\ & =\frac{1}{\pi}\left[\frac{1}{n+1}\left(1-\left(-1\right)^{n+1}\right)+\frac{1}{n-1}\left(1-{(-1)}^{n-1}\right)\right] \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-0a25f0489e2163897837f82b327752d2_l3.png)
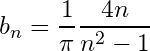
![Rendered by QuickLaTeX.com \[b_1=\frac{1}{\pi}\int_{0}^{\pi}\sin{2x\ dx=0}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-29db1fe904f7ed78dc2de2fef85d3906_l3.png)
![Rendered by QuickLaTeX.com \[b_n=\left\{\begin{matrix}0,\ \ \ \ \ \ \ \ \ \ \ \ \ n\text{ is odd}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\\frac{1}{\pi}\frac{4n}{n^2-1},\ n\text{ is even },\ n\in\mathbb{N}\\\end{matrix}\right.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-41e7b9f40f29259437d65e2751ff85a4_l3.png)
![Rendered by QuickLaTeX.com \[\frac{4}{\pi}\left[\frac{2}{1\cdot3}\sin{2x+\frac{4}{3\cdot5}\sin{4x+\frac{6}{5\cdot7}\sin{6x+\ldots}}}\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d9fb9f9943b5c4aad642b959a6dd5605_l3.png)
![Rendered by QuickLaTeX.com \[f\left(\frac{\pi}{4}\right)=\frac{1}{\sqrt2}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1140cefe356ee361f3a84dd844389fb3_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \frac{1}{\sqrt2} & =\frac{4}{\pi}\left[\frac{2}{1\cdot3}-\frac{6}{5\cdot7}+\frac{10}{9\cdot11}-\ldots\right]\\ & \Rightarrow\frac{2}{1\cdot3}-\frac{6}{5\cdot7}+\frac{10}{9\cdot11}-\ldots=\frac{\pi}{4\sqrt2}\ \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e1fd6a800f9f4f5dc67edf9d58937197_l3.png)
![Rendered by QuickLaTeX.com \[\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx=0.}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d8baea6c51d8a3bf2b5663fc4e7afd96_l3.png)
![Rendered by QuickLaTeX.com \[a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)dx=0,}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-59396c9c54e8e0fe164ac2c5489c7335_l3.png)
![Rendered by QuickLaTeX.com \[a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\cos{nx\ dx=0\ \left(n\in\mathbb{N}\right).}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-517b10b2c0c71d3c4b6a67fb45926c91_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\pi}{2}-\frac{4}{\pi}\left\{\cos{x+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots}\right\}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-7174beddffc310986cc2907990b3ac84_l3.png)
![Rendered by QuickLaTeX.com \[1+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+\ldots=\frac{\pi^2}{8}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8f2960a6727501fb2d874c0b8c12e96d_l3.png)
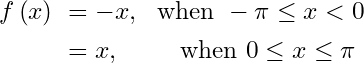
![Rendered by QuickLaTeX.com \[a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)dx=\frac{2}{\pi}\ \int_{0}^{\pi}{x\ dx\ \ (\because\ \left|x\right|\text{ is even})}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b48bd2af0fcad06808dd094b15cd5d09_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} n\in\mathbb{N},\ {\ a}_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\cos{nx}dx=\frac{2}{\pi}\ \int_{0}^{\pi}{x\ \cos{nx}dx}}\\ a_n & =\frac{2}{\pi}\left\{\left[\frac{x}{n}\sin{nx}\right]_0^\pi-\frac{1}{n}\int_{0}^{\pi}\sin{nx\ dx}\right\}\\ a_n & =\frac{2}{n^2\pi}[\cos n\pi-1] \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1fea6a0af9e2cda6f1641eeeaee431ca_l3.png)
![Rendered by QuickLaTeX.com \[a_n=\left\{\begin{matrix}\ \ \ \ \ \ 0\ \ ,\ \ \text{ for } n\text{ is even}\\-\frac{4}{n^2\pi},\ \ \text{ for } n\text{ is odd}\\\end{matrix}\right.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e6d96a6f85cbaaacb239029b0e379c89_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\pi}{2}-\frac{4}{\pi}\left[\frac{\cos{x}}{1^2}{+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots}\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8a2437f5a006b68f01cf1b5c98f64677_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}\left[f\left(-\pi+0\right)+f\left(\pi-0\right)\right]=\pi,\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-ec1832c6ef323e0d5a60282d939dcc17_l3.png)
![Rendered by QuickLaTeX.com \[\left|x\right|=\frac{\pi}{2}-\frac{4}{\pi}\left[\frac{\cos{x}}{1^2}{+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots}\right],\ x\in\left[-\pi,\ \pi\right].\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-61b4f8959fb54eef8d2bf01a83969899_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} f\left(0\right) & =\frac{\pi}{2}-\frac{4}{\pi}\left[\frac{1}{1^2}{+\frac{1}{3^2}+\frac{1}{5^2}+\ldots}\right]\\ \Rightarrow & \frac{\pi}{2}-\frac{4}{\pi}\left[\frac{1}{1^2}{+\frac{1}{3^2}+\frac{1}{5^2}+\ldots}\right]=0\\ \Rightarrow & \frac{\pi}{2}=\frac{4}{\pi}\left[\frac{1}{1^2}{+\frac{1}{3^2}+\frac{1}{5^2}+\ldots}\right] \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-cdbc5dd55e19b482c4bffa32b658bb04_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow\frac{\pi^2}{8}=\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+\ldots\textbf{ (We got our requird result)}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8ee5631a2da11e228b87a708e64d7d5c_l3.png)
![Rendered by QuickLaTeX.com \[\frac{4\sin{h\pi}}{\pi}\left[\frac{\sin{x}}{1^2+1}-\frac{2\sin{2x}}{2^2+1}+\frac{3\ \sin{3x}}{3^2+1}-\ldots\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-f2274e7e79fa6e54b38f4f8997f9994b_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{1^2+1}-\frac{3}{3^2+1}+\frac{5}{5^2+1}-\frac{7}{7^2+1}+\ldots=\frac{\pi}{4\cos{h\frac{\pi}{2}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-3bff777844141ac1a59a1464ac277c6a_l3.png)
![Rendered by QuickLaTeX.com \[\bm{\sum_{n=1}^{\infty}{b_n\sin{nx}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-cbf01db2ef12afb976cd8a208fcf5618_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} b_n & =\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left(x\right)\sin{nx\ dx}}\\ & =\frac{2}{\pi}\int_{0}^{\pi}{\left(e^x-e^{-x}\right)\sin{nx\ dx}}\\ & =\frac{2}{\pi}\left[\frac{e^x}{n^2+1}(\sin{nx-n\cos{nx)-\frac{e^{-x}}{n^2+1}(-\sin{nx-n\cos{nx)}}}}\right]_0^\pi\\ b_n & =\frac{2}{\left(n^2+1\right)\pi}\left(e^\pi-e^{-\pi}\right)\cos{n\pi,\ \ \ n\in\mathbb{N}} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-7d1c3f0739d181ab27d17c351c51b662_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2}{\pi}(e^\pi-e^{-\pi})\left[\frac{1}{1^2+1}\sin{x}-\frac{2}{2^2+1}\sin{2x}+\frac{3}{3^2+1}\sin{3x}-\ldots\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-84561b4fad173255c1e5ee883cc9f84a_l3.png)
![Rendered by QuickLaTeX.com \[\bm{e^x-e^{-x}=\frac{4}{\pi}\sin{h\pi\left[\frac{\sin{x}}{1^2+1}-\frac{2\sin{2x}}{2^2+1}+\frac{3\ \sin{3x}}{3^2+1}-\frac{4\sin{4x}}{4^2+1}+\ldots\right]}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-27da7d28bec6383049896374fcb99f58_l3.png)
![Rendered by QuickLaTeX.com \[\bm{e^\frac{\pi}{2}-e^{-\frac{\pi}{2}}=2\sin{h\frac{\pi}{2}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-350374ce89028ee97fd2c3cd73b5cd53_l3.png)
![Rendered by QuickLaTeX.com \[\bm{\frac{1}{1^2+1}-\frac{3}{3^2+1}+\frac{5}{5^2+1}-\frac{7}{7^2+1}+\ldots=\frac{\pi}{4\cos{h\frac{\pi}{2}}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-77290bf967aa4710fc140cc872a9abbf_l3.png)
![Rendered by QuickLaTeX.com \[\bm{\frac{1}{2}a_0+\sum_{n=1}^{\infty}{a_n\cos{nx}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-0260ba08e2153336d2fa042157873938_l3.png)
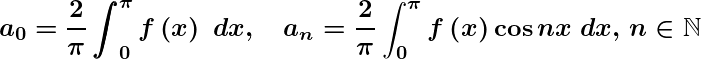
![Rendered by QuickLaTeX.com \[\dfrac{\bm{1}}{\bm{2}}\bm{a_0+\sum_{n=1}^{\infty}a_{n}\cos{nx}=}\dfrac{\bm{1}}{\bm{2}}\bm{[f(x+0)+f(x-0)]}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-fdefa4f5f62df5521701c9a36702d49f_l3.png)
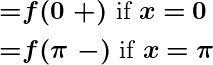
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{b_n\sin{nx}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-998104f3aaad60d0da69535df75a512e_l3.png)
![Rendered by QuickLaTeX.com \[b_n=\frac{2}{\pi}\int_{0}^{\pi}{f\left(x\right)\sin{nx\ dx,}}\ n\in\mathbb{N}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b70ba5d7bf2249e38d4686b7ef3640ca_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \sum_{n=1}^{\infty}b_{n}\sin{nx} & =\dfrac{1}{2}[f(x+0)+f(x-0)]\text{ if } x\in(0, \ \pi)\\ & = 0 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{ if } x=0 \text{ or } \pi \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-efd7a136f8d34a7169da869b57bf8d53_l3.png)
![Rendered by QuickLaTeX.com \[F\left(x\right)=\begin{cases} f(-x) \text{ if } x\in[-\pi,\ 0]\\ f(x) \;\;\; \text{ if } x\in [0,\ \pi] \end{cases}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-3cfe9f9b8dc57e3001a5bc8aeb111977_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2}a_0+\sum_{n=1}^{\infty}{a_n\cos{nx}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-74ae1333ba76cca34b5f10961b4f2f92_l3.png)
![Rendered by QuickLaTeX.com \[a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}{F\left(x\right)dx=\frac{2}{\pi}\int_{0}^{\pi}{f\left(x\right)dx\ (\because F\ \text{is even})}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e1caa75df7ae6a8a9450423d186c62c8_l3.png)
![Rendered by QuickLaTeX.com \[a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{F\left(x\right)\cos{nx}dx=\frac{2}{\pi}\int_{0}^{\pi}{f\left(x\right)\cos{nx}dx\ (n\in\mathbb{N})}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-66f37bb47cb7d3a09bc3807b803fe695_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} & \frac{1}{2}a_0+\sum_{n=1}^{\infty}{a_n\cos{nx}}=\frac{1}{2}[F\left(x+0\right)+F\left(x-0\right)]\\ & =\frac{1}{2}\left[f\left(x+0\right)+f\left(x-0\right)\right]\ \text{ for }\ x\in(0,\ \pi)\\ & =\frac{1}{2}\left[F\left(0+\right)+F\left(0-\right)\right]=f\left(0+\right)\ \text{ for }\ x=0\\ & =\frac{1}{2}\left[F\left(-\pi+0\right)+F\left(\pi-0\right)\right]=f\left(\pi-0\right)\ \text{ for }\ x=\pi\\ \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2cbde86cd0a5a611cce77550464e3d84_l3.png)
![Rendered by QuickLaTeX.com \[F\left(x\right)=\begin{cases} -f(-x) \text{ if } [-\pi,\ 0]\\ f(x) \;\;\;\;\; \text{ if } [0,\ \pi] \end{cases}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5aa2b216d02c6759a92b7da473d66ac9_l3.png)
![Rendered by QuickLaTeX.com \[b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{F\left(x\right)\sin{nx\ dx}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-6bb9768c6de538341e2905836407b1c2_l3.png)
![Rendered by QuickLaTeX.com \[b_n=\frac{2}{\pi}\int_{0}^{\pi}{f\left(x\right)\sin{nx\ dx}}\ (n\in\mathbb{N})\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-896429ce40a5d26efce3c7de9f0ca672_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \sum_{n=1}^{\infty}{b_n\sin{nx}} & =\frac{1}{2}[F\left(x+0\right)+F\left(x-0\right)]\\ & =\frac{1}{2}\left[f\left(x+0\right)+f\left(x-0\right)\right],\ \text{ for }\ x\in(0,\ \pi)\\ & =\frac{1}{2}\left[F\left(0+\right)+F\left(0-\right)\right]=0,\ \text{ for }\ x=0\\ & =\frac{1}{2}\left[F\left(-\pi+0\right)+F\left(\pi-0\right)\right]=0,\ \text{ for }\ x=\pi \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8f83997a747218355b8cba2acfbbb49d_l3.png)
![Rendered by QuickLaTeX.com \[x\left(\pi-x\right)=\frac{8}{\pi}\left(\frac{\sin{x}}{1^3}+\frac{\sin{3x}}{3^3}+\frac{\sin{5x}}{5^3}+\ldots\right)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-4d914875712ed0f376d973134380af81_l3.png)
![Rendered by QuickLaTeX.com \[x=\frac{\pi}{2}-\frac{4}{\pi}\left(\frac{\cos{x}}{1^2}+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots\right),\ 0\leq x\leq\pi\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c3d2c5df2b1a75f70fece6d78662b219_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} b_n & =\frac{2}{\pi}\int_{0}^{\pi}{x\left(\pi-x\right)\sin{nx\ dx\ (n\in\mathbb{N})}}\\ & =\frac{2}{\pi}\left[\pi\left\{\left[-\frac{x}{n}\cdot\cos{nx}\right]_0^\pi+\frac{1}{n}\int_{0}^{\pi}\cos{nx\ dx}\right\}-\left\{\left[-\frac{x^2}{n}\cdot\cos{nx}\right]_0^\pi+\frac{2}{n}\int_{0}^{\pi}x\cos{nx\ dx}\right\}\right]\\ & =\frac{2}{\pi}\left[-\frac{\pi^2}{n}\cos{n\pi+}\frac{\pi^2}{n}\cos{n\pi-\frac{2}{n}\left\{\left[\frac{x\sin{nx}}{n}\right]_0^\pi-\frac{1}{n}\int_{0}^{\pi}\sin{nx\ dx}\right\}}\right]\\ & =\frac{4}{\pi n^3}(1-\cos{n\pi),\ \ \ (n\in\mathbb{N})} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d47004d27560dbec473d809e67994227_l3.png)
![Rendered by QuickLaTeX.com \[x\left(\pi-x\right)=\frac{8}{\pi}\left[\frac{\sin{x}}{1^3}+\frac{\sin{3x}}{3^3}+\frac{\sin{5x}}{5^3}+\ldots\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1eeeb7b9092127d99da543a083d5d21c_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\cos{x}}{1^2}+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots=\sum_{n=1}^{\infty}\frac{\cos{\left(2n-1\right)x}}{\left(2n-1\right)^2}, \text{ is uniformly convergent.}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-567758d1c238a3483c20b9cb747bd6d6_l3.png)
![Rendered by QuickLaTeX.com \[\left|\frac{\cos{\left(2n-1\right)x}}{{(2n-1)}^2}\right|\le\frac{1}{{(2n-1)}^2}\le\frac{1}{n^2}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-38f2ae8d43488addf455753535fd32fd_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{x=1}^{\infty}\frac{1}{n^2}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b8cb8b63be2ce29cb2ffdcee9030d8b0_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\cos{x}}{1^2}+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-02790baa59b51c28508b00ca28a61b6f_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\sin{x}}{1^3}+\frac{\sin{3x}}{3^3}+\frac{\sin{5x}}{5^3}+\ldots\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1b30ce861d7004e67a0930a80f5d0e41_l3.png)
![Rendered by QuickLaTeX.com \[\frac{8}{\pi}\left[\frac{\sin{x}}{1^3}+\frac{\sin{3x}}{3^3}+\frac{\sin{5x}}{5^3}+\ldots\right]\text{ converges to } x\left(\pi-x\right)\text{ in } \left[0,\ \pi\right].\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c2e9a45da443c4265302ba6f8a4e565f_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \pi-2x & =\frac{8}{\pi}\left[\frac{\cos{x}}{1^2}+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots\right]\\ \Rightarrow x & =\frac{\pi}{2}-\frac{4}{\pi}\left[\frac{\cos{x}}{1^2}+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\ldots\right],\text{ for } 0\le x\le\pi \\ \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-54cec42c0bd5512587a98fd08f1bfa5a_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{\frac{\cos{nx}}{n^2}=\frac{3x^2-6\pi x+2\pi^2}{12}}\ (0\le x\le\pi)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2a50be6d9f73bc09a58820ea3397e9f2_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} a_0 & =\frac{2}{\pi}\int_{0}^{\pi}{f\left(x\right)\ dx=\pi\ \ }\\ a_n & =\frac{2}{\pi}\int_{0}^{\pi}{f\left(x\right)\cos{nx\ dx=\frac{2}{\pi}\int_{0}^{\pi}{x\cos{nx\ dx}}}}\\ & =\frac{2}{\pi}\left\{\left[\frac{x\sin{nx}}{n}\right]_0^\pi-\frac{1}{n}\int_{0}^{\pi}\sin{nx\ dx}\right\}\\ & =-\frac{2}{\pi n^2}(1-\cos{n\pi),\ \ \ n\in\mathbb{N}} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-004c846e90c393971d446fb1cb812b36_l3.png)
![Rendered by QuickLaTeX.com \[x=\frac{\pi}{2}-\frac{4}{\pi}\sum_{n=\text{odd}}{\frac{\cos{nx}}{n^2}\ \ldots(1)}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9d5c5b76939733f822802cb5a3500243_l3.png)
![Rendered by QuickLaTeX.com \[a_0=\frac{2}{\pi}\int_{0}^{\pi}{x^2\ dx={\frac{2}{3}\pi}^2\ \ }\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d90c8eaa11f6205921a43b0734b4315c_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} a_n= & \frac{2}{\pi}\int_{0}^{\pi}{x^2\cos{nx\ dx=\frac{2}{\pi}\left\{\left[\frac{x^2}{n}\sin{nx}\right]_0^\pi-\frac{2}{n}\int_{0}^{\pi}x\sin{nx\ dx}\right\}}}\\ & =-\frac{4}{n\pi}\left\{\left[-\frac{x\cos{nx}}{n}\right]_0^\pi+\frac{1}{n}\int_{0}^{\pi}\cos{nx\ dx}\right\}\\ & =\frac{4}{n^2}\cos{n\pi,\ \ \ n\in\mathbb{N}} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9e1ffe9232880a93fdb509fada6116d0_l3.png)
![Rendered by QuickLaTeX.com \[x^2=\frac{\pi^2}{3}+4\sum_{n=1}^{\infty}{\frac{\cos{nx\cos{n\pi}}}{n^2}\ldots(2)}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-09fa7d97bf54d623da127b40955c05e9_l3.png)
![Rendered by QuickLaTeX.com \[2\sum_{n=\text{odd}}{\frac{\cos{nx}}{n^2}=\frac{\pi(\pi-2x)}{4}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b0203ec26dbc8c4686738bd5c0e4db6a_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{{(-1)}^n\frac{\cos{nx}}{n^2}=\frac{3x^2-\pi^2}{12}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-f4d9b3229fbadd8257e53a4bbf179218_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{\frac{\cos{nx}}{n^2}=\frac{3x^2-6\pi x+2\pi^2}{12}\ \ \ (0\le x\le\pi)}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-bee3b3b6e7ff96dc595853f1e382bd1d_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)=\begin{cases} \;\;\; \dfrac{\pi}{3},\;\;\;\;\; 0\le x\le\dfrac{\pi}{3}\\ \;\;\; 0,\;\;\;\;\; \dfrac{\pi}{3}<x<\dfrac{2\pi}{3}\\ -\dfrac{\pi}{3},\;\;\; \dfrac{2\pi}{3}<x\le\pi \end{cases}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-da045047bcc1d231360b4d8955ca1063_l3.png)
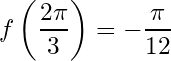
![Rendered by QuickLaTeX.com \[1-\frac{1}{5}+\frac{1}{7}-\frac{1}{11}+\frac{1}{13}-\frac{1}{17}+\ldots=\frac{\pi}{2\sqrt{3}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1068cec2afe0eea45b489bfd05995580_l3.png)
![Rendered by QuickLaTeX.com \[a_0 =\frac{2}{\pi}\int_{0}^{\pi}{f\left(x\right)dx=\frac{2}{\pi}\left[\int_{0}^{\frac{\pi}{3}}{\frac{\pi}{3}dx+\int_{\frac{2\pi}{3}}^{\pi}\left(-\frac{\pi}{3}\right)dx}\right]=\frac{2}{\pi}\left[\frac{\pi^2}{9}-\frac{\pi^2}{9}\right]}=0\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-be7d9e6e8b54934069ac3bf27e761c05_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} a_n & =\frac{2}{\pi}\int_{0}^{\pi}{f(x)\cos{nx\ dx=\frac{2}{\pi}\left[\frac{\pi}{3}\int_{0}^{\frac{\pi}{3}}\cos{nx\ dx}-\frac{\pi}{3}\int_{\frac{2\pi}{3}}^{\pi}\cos{nx\ dx}\right]}}\\ a_n & =\frac{2}{3}\left[\frac{1}{n}\sin{\frac{n\pi}{3}-\frac{1}{n}\left(\sin{n\pi-\sin{\frac{2n\pi}{3}}}\right)}\right]\\ a_n & =\frac{2}{3n}\left[\sin{\frac{n\pi}{3}+\sin{\frac{2n\pi}{3}}}\right]=\frac{4}{3n}\sin{\frac{n\pi}{2}\cos{\frac{n\pi}{6}}}\\ a_n & =\frac{4}{3n}\sin{\frac{n\pi}{2}\cos{\frac{n\pi}{6}}}, \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-3cef0423b15596627c39d606ded1a3c9_l3.png)
![Rendered by QuickLaTeX.com \[\frac{4}{3}\sum_{n=1}^{\infty}{\frac{1}{n}\sin{\frac{n\pi}{2}\cos{\frac{n\pi}{6}\cos{nx}}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-6aecb127f9feb173cf5587a222e7de55_l3.png)
![Rendered by QuickLaTeX.com \[\frac{4}{3}\left[\cos{\frac{\pi}{6}\cos{x-\frac{1}{5}\cos{\frac{\pi}{6}\cos{5x+\frac{1}{7}\cos{\frac{\pi}{6}\cos{7x-\frac{1}{11}\cos{\frac{\pi}{6}\cos{11x+\ldots}}}}}}}}\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c1ef8bba20bb626814f5d2d6c31fb44e_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2}{\sqrt3}\left[\frac{\cos{x}}{1}-\frac{\cos{5x}}{5}+\frac{\cos{7x}}{7}-\frac{\cos{11x}}{11}+\ldots\right]\ (0\le x\le\pi)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-ffd666519b7138b98f2480d2f0ded7b4_l3.png)
![Rendered by QuickLaTeX.com \[1-\frac{1}{5}+\frac{1}{7}-\frac{1}{11}+\ldots=\frac{\pi}{2\sqrt3}.\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-ee4307ef73d19e4341c8f07d000c77f8_l3.png)
![Rendered by QuickLaTeX.com \[a_0=\frac{2}{\pi}\int_{0}^{\pi}f(x)dx=\dfrac{2}{c\pi}[1-\cos{c\pi}]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2ec536669c5e15cadd94090a813a3daf_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} a_n & =\frac{2}{\pi}\int_{0}^{\pi}{f\left(x\right)\cos{nx\ dx=\frac{2}{\pi}\int_{0}^{\pi}\sin{cx\cos{nx\ dx}}}}\\ & =\frac{1}{\pi}\int_{0}^{\pi}[\sin(c+n)x+\sin(c-n)x]dx\\ & =\frac{1}{\pi}\left[\frac{1-\cos{(c+n)\pi}}{c+n}+\frac{1-\cos{(c-n)\pi}}{c-n}\right]\\ a_n & =\frac{1}{\pi}\left[\frac{1-\left(-1\right)^n\cos{c\pi}}{c+n}+\frac{1-\left(-1\right)^n\cos{c\pi}}{c-n}\right]\\ \bm{\therefore a_n} & \bm{=} \frac{\bm{2c(1+\cos{c\pi)}}}{\bm{\pi}}\bm{\cdot}\frac{\bm{1}}{\bm{c^2-n^2}}\textbf{, where } \bm{n}\textbf{ is odd} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1b89c6eec2404b9e13ad69105f9c66ad_l3.png)
![Rendered by QuickLaTeX.com \[\bm{a_n=}\frac{\bm{2c(1-\cos{c\pi)}}}{\bm{\pi}}\bm{\cdot}\frac{\bm{1}}{\bm{c^2-n^2}}\textbf{, when }\bm{n} \textbf{ is even.}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1b430e402e322de3fe9fd4aa2ec17603_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1-\cos{c\pi}}{\pi}\left[\frac{1}{c}+2c\sum_{n=1}^{\infty}\frac{\cos{2nx}}{c^2-4n^2}\right]+\frac{2c(1+\cos{c\pi)}}{\pi}\sum_{n=1}^{\infty}\frac{\cos{\left(2n-1\right)x}}{c^2-{(2n-1)}^2}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e11bf69997c0c26166e5fe6fa9a6d694_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}{\frac{{(-1)}^n}{n^2+1}=\frac{1}{2}\ [\pi\ \text{cosech}}\ \pi-1]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-f6a62cc26d72320a536c7ea3453a1dec_l3.png)
![Rendered by QuickLaTeX.com \[a_0=\frac{1}{\pi}\int_{0}^{2\pi}{f\left(x\right)dx=\frac{1}{\pi}\left[e^{2\pi}-1-2\pi\right]}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b002953efa3aec601faf73c50ea93413_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} a_n & =\frac{1}{\pi}\int_{0}^{2\pi}{f\left(x\right)\cos{nx\ dx}}\\ & =\frac{1}{\pi}\int_{0}^{2\pi}{\left(e^x-1\right)\cos{nx\ dx}}\\ & =\frac{1}{\pi}\left[\frac{e^x}{n^2+1}(\cos{nx+n\sin{nx)}}\right]_0^{2\pi}\\ & =\frac{1}{\pi(n^2+1)}\left[e^{2\pi}-1\right],\ n\in\mathbb{N} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-a50e1b406de4d540b95d4324db755c6c_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} b_n & =\frac{1}{\pi}\int_{0}^{2\pi}{f\left(x\right)\sin{nx\ dx}}\\ & =\frac{1}{\pi}\int_{0}^{2\pi}{(e^x-1)\sin{nx\ dx}}\\ & =\frac{1}{\pi}\left[\frac{e^x}{n^2+1}(\sin{nx-n\cos{nx)}}\right]_0^{2\pi}\\ & =\frac{1}{\pi(n^2+1)}\left[n-ne^{2\pi}\right],\ n\in\mathbb{N} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b6966a4140d107306c8b26076a3d1118_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{2\pi}\left[e^{2\pi}-2\pi-1\right]+\frac{e^{2\pi}-1}{\pi}\sum_{n=1}^{\infty}{\frac{1}{n^2+1}\cos{nx+\frac{1-e^{2\pi}}{\pi}\sum_{n=1}^{\infty}{\frac{n}{n^2+1}\cdot\sin{nx}}}}\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5aaf8efcda781f391600f74c3680f1b3_l3.png)
![Rendered by QuickLaTeX.com \[-1+\frac{e^{2\pi}-1}{\pi}\left[\frac{1}{2}+\sum_{n=1}^{\infty}\frac{(\cos{nx-n\sin{nx)}}}{n^2+1}\right]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d8de9985f690442c1f1e0eb79c595d98_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}\dfrac{(-1)^{n}}{n^{2}+1}=\dfrac{\pi e^{\pi}}{e^{2\pi}-1}-\dfrac{1}{2}=\dfrac{1}{2}[\pi \text{ cosech } \pi-1]\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-21518f8a62d7e8105880b154ef54871a_l3.png)