Introduction:
The Riemann integral of a bounded function over a closed, bounded interval is defined using approximations of the function that are associated with partitions of its domain into finite collections of subintervals. The generalization of the Riemann integral to the Lebesgue integral will be achieved by using approximations of the function that are associated with decompositions of its domain into finite collections of sets which we call Lebesgue measurable. Each interval is Lebesgue measurable. The richness of the collection of Lebesgue measurable sets provides better upper and lower approximations of a function, and therefore of its integral than are possible by just employing intervals. This leads to a larger class of functions that are Lebesgue integrable over very general domains and an integral that has better properties. For instance, under quite general circumstances we will prove that if a sequence of functions converges point-wise to a limiting function, then the integral of the limit function is the limit of the integrals of the approximating functions.
Motivation:
One of the primary motivations for developing a theory has to do with the failure of the theory of Riemann integration to behave nicely undertaking point-wise limits of functions. In particular, it is well-known that point-wise convergence of a sequence of functions does not translate to the interchange of limits and integrals; for example, if ![Rendered by QuickLaTeX.com [f_{n}(x)=begin{cases} 1, ;;; & text{when } xin [n,n+1] \ 0, ;;; & text{otherwise } end{cases}]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-0745654d10763ad2e084992ab848a332_l3.png)
,
converges pointwise to the zero function.
If we take its integral, Which leads to
. This inability to interchange a limit and an integral can be extremely inconvenient. One can interchange a limit and Riemann integration under certain circumstances like uniform convergence, but this is usually far too restrictive of a condition. What measure-theoretic integration gives you is a way to do this interchange provided we, have point-wise convergence and much weaker conditions than uniform convergence; in exchange, it forces us to throw out sets of measure zero. In addition, once the theory is developed we suddenly have extremely powerful tools to take limits of integrals you did not have before (Lebesgue dominated convergence theorem). So we have two main motivations to make a rich theory
- To integrate more functions (Like Dirichlet Function )
- To make space this is completely integrable.
There are more motivations like
- Interchanging limits and integrals (e.g. the limit of a sequence of continuous functions may not be Riemann integrable)
- Length of Curves (finding the length of curves that are only rectifiable, not continuously differentiable), etc.
Definition:
To define Lebesgue Measure on a set we need some precious definitions and some important functions and classes or collections of subsets of ![]() .
.
Length Function:
Let denote the collection of all intervals of
![]() . If an interval
. If an interval has endpoints
and
we write it as
. By convention, the open interval
. Let

by [lambda((a,b))=begin{cases} vert b-avert, ;;; & text{if } a,bin mathbb{R} \ +infty, ;;; & text{if either } a=-infty text{ or } b=+infty text{ or both} end{cases}] This
is called length function defined on
.
Properties of Set Function:
is monotonic i.e.
is finitely additive.
Let be such that
where
for
Then [lambda(I)=sum_{i=1}^{n}lambda(J_{i}) ]
is finitely sub-additive.
Let be such that
Then [lambda(I)leq sum_{i=1}^{n}lambda(J_{i}) ]
is countable additive .
Let be such that
where
for
Then [lambda(I)= sum_{i=1}^{infty}lambda(J_{i}) ]
is countable sub-additive .
Let be such that
where Then [lambda(I)leq sum_{i=1}^{infty}lambda(J_{i}) ]
- Translation Invariance
[lambda(I)=lambda(I+x),] For every and
.
Algebra on a set:
Let be any non-empty set and let
a collection of subsets of
. Then the collection
is called an algebra of subsets of
if
satisfies following properties:
whenever
whenever
Then is called Algebra on
.
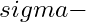 Algebra on a set:
Algebra on a set:
Let be any non-empty set and let
a collection of subsets of
. Then the collection
is called an
![]() Algebra of subsets of
Algebra of subsets of if
satisfies following properties:-
whenever
for
Then is called
![]() Algebra on
Algebra on .
Definition of Lebesgue Measure:
Def:- For every subsets of
![]() , the Lebesgue Outer Measure of
, the Lebesgue Outer Measure of , denoted by
is defined by [displaystylemathit{m}^{*}(A)=infleftlbracesum_{i=1}^{infty}lambda(I_{i}):Asubsetbigcup_{i=1}^{n}I_{i}rightrbrace] Where
varies over all possible sequence of open intervals of
![]() whose union contains
whose union contains .
Properties of Lebesgue Outer Measure:
The Lebesgue Outer Measure is generated by length function which is defined on earlier so it’s preserves some of their properties.
is monotonic i.e.
is finitely sub-additive .
Let be such that
Then [mathit{m}^{*}(I)leq sum_{i=1}^{n}mathit{m}^{*}(J_{i}) ]
is countable sub-additive .
Let be such that
where Then [mathit{m}^{*}(I)leq sum_{i=1}^{infty}mathit{m}^{*}(J_{i}) ]
- Translation Invariance
[mathit{m}^{*}(I)=mathit{m}^{*}(I+x),] For every and
. Now we already noticed that
hasn’t had the properties of finitely additive and not countable additive (why?) A Vitali* Set in
, has a positive measure Specifically, let
denote translation. (textit{That is, for
and
let
}.) Note that outer measure
is invariant under translation, so [mathit{m}^{*}(Aoplus x)=mathit{m}^{*}(A)] Now let
be a Vitali set, and let
be an enumeration of the rationals in
. By construction of
, the sets
are pair wise disjoints and their union is
. By countable sub-additively we have
In particular we must have So we can find an integer
sufficiently large that [N.mathit{m}^{*}(V)>1, text{ For } n=1,ldots,N], Let
. Then the sets
are pair wise disjoint, and since
We have [E=bigcup_{n=1}^{N}E_{n}]. Hence by monotonicity,
. On the other hand, [sum_{n=1}^{N}mathit{m}^{*}(E_{n})=sum_{n=1}^{N}mathit{m}^{*}(Voplus q_{n})=sum_{n=1}^{N}mathit{m}^{*}(V)=N.mathit{m}^{*}(V)>1.] So we have [mathit{m}^{*}(E)<sum_{n=1}^{N}mathit{m}^{*}(E_{n})] So we saw that
is not finitely additive and it is also not countable sub-additive. Vitali: An elementary example of a set of real numbers which is not Lebesgue measurable. Definition: Measurable Set(Carathéodory Condition): A set
is said to be Lebesgue-Measurable if [mathit{m}^{*}(A)=mathit{m}^{*}(Acap E)+mathit{m}^{*}(Acap E^{c}) text{ for all } Asubset mathbb{R}] This Condition is known as Carathéodory Condition.
Properties of Measurable set in R
- If
is Lebesgue Measurable then
also Lebesgue Measurable set in
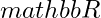
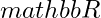 and
and are Lebesgue Measurable
- Every Interval in
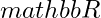 is Lebesgue Measurable.
is Lebesgue Measurable. - Every countable set is Lebesgue Measurable with measure zero i.e.
If is a countable set in
![]() then [mathit{m}^{*}(B)=0.]
then [mathit{m}^{*}(B)=0.]
- Every uncountable set has a non-zero measure (except Cantor Set)
- Every Borel* set is Lebesgue Measurable.
(Borel Set: Collection of all and
sets) Definition: Class
![]() :- Collection of all Lebesgue Measurable sets in
:- Collection of all Lebesgue Measurable sets in ![]() . [mathcal{M}=lbrace E; : ; text{E is Lebesgue meusurable in }mathbb{R}; Esubseteqmathbb{R} rbrace] This Collection
. [mathcal{M}=lbrace E; : ; text{E is Lebesgue meusurable in }mathbb{R}; Esubseteqmathbb{R} rbrace] This Collection ![]() is a
is a ![]() Algebra and it is the largest measurable
Algebra and it is the largest measurable ![]() Algebra over
Algebra over ![]() and (
and (![]() ) is called Measure Space which we want to achive.
) is called Measure Space which we want to achive.
Conclusion:
Now we got a new developed theory on subsets of ![]() and we can now use the theory to integrate those kinds of functions which we can’t integrate by using Riemann Integration. Also, we can use the theory to find the length of those kinds of curves which is not continuously differentiable on
and we can now use the theory to integrate those kinds of functions which we can’t integrate by using Riemann Integration. Also, we can use the theory to find the length of those kinds of curves which is not continuously differentiable on ![]() and we can use to find the integration over rationalize functions too. This rich theory gave us more freedom to apply on the space or subsets in
and we can use to find the integration over rationalize functions too. This rich theory gave us more freedom to apply on the space or subsets in ![]() .
.
Bibliography:
- Yeh ; Real Analysis
- Robert G. Bartle; The Elements of Integration and Lebesgue Measure.
- Sheldon Axler; Measure, Integration, and Real Analysis.
Thank You. Don’t forget to join us on our Facebook page for any new articles and a lot more!!!!!
