Introduction:
The story of integration started with I. Newton, when in the late 1660 he invented the method of inverse tangents to find areas under curves. In 1680, G. Leibnitz discovered the process of finding tangent line to find area. Thus, they had discovered the integration, being a process of summation, was inverse to the operation of differentiation since finding tangent lines involved differences and finding areas involved summations. In 1854, G.F Riemann formulated a new and different approach to define integral on the real line. He separated the concept from its differentiation. His approach was to examine the motivating summation and limit process of finding areas by itself. In 1875, J.G Darboux viewed Riemann Integration in a different way. The approaches of both Riemann and Darboux demanded the integration to be bounded in its domain. It has been established that the two definitions of definite integral given by Riemann and Darboux are equivalent that is why Riemann integral are often called Darboux-Riemann Integrals. In this article we will discuss about the integral based on Riemann and Darboux-Riemann approach will be discussed in mainly on real line ().
- Definition:
Partition: Let be a given closed and bounded on real line. Let
be finite number of points in
such that
P = lbrace x_{0}, x_{1}, x_{2}, ldots, x_{n} rbrace
[a, b]
[a, b]
n
[ x_{i-1}, x_{i} ]
i=1,2,ldots, n
P
[a, b]
a
b
[a, b]
P = [a, b]
[a, b]

[a, b]
[a, b]
P [a, b]
pin P[a, b]
p
[a, b]
n
p_{1}=leftlbrace 0,dfrac{1}{n},dfrac{2}{n},cdots , dfrac{n-1}{n} , 1 rightrbrace
[0,1]p_{2}=leftlbrace 0,dfrac{1}{2n},dfrac{2}{2n},cdots , dfrac{2n-1}{2n} , 1 rightrbrace
[0,1]p_{3}=leftlbrace 0,dfrac{1}{3n},dfrac{2}{3n},cdots , dfrac{3n-1}{3n} , 1 rightrbrace
[0,1]
1notin P
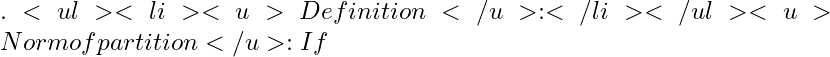
[a, b]
I_{r}= [x_{r-1},ldots, x_{r},]
[a, b]
r=1, 2, …, n
delta r = vert I_{r}vert =(x_{r}-x_{r-1})
r=1, 2, ldots, n
max lbrace vert I_{r} vert ; : ; r=1, 2, ldots, n rbrace
p
delta
Vert P Vert
delta = max lbrace delta_{r} : r = 1, 2, ldots, nrbrace
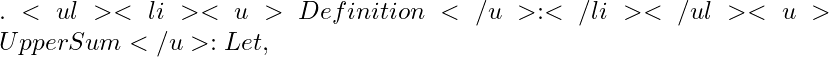
[a, b]
P = lbrace x_{0}, x_{1}, x_{2}, ldots, x_{n} rbrace
[a, b]
f
[ x_{r-1}, x_{r} ] (r=1, 2, ldots, n)
M_{r}=suplbrace f(x) ; : ; x in [ x_{r-1}, x_{r} ] rbrace
displaystylesum_{r=1}^{n}M_{r}delta_{r}
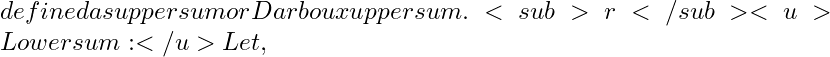
[a, b]
P = lbrace x_{0}, x_{1}, x_{2}, ldots, x_{n} rbrace
[a, b]
m_{r}=inflbrace f(x) ; : ; x in [ x_{r-1}, x_{r} ] rbrace
displaystylesum_{r=1}^{n}m_{r}delta_{r}
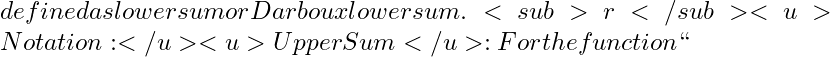
p
[a, b]
fp
[a, b]
U(p,f)L(p,f)
f(x)
fp
[a, b]
f[a, b]
pin P[a,b]
mM
f
[a, b]
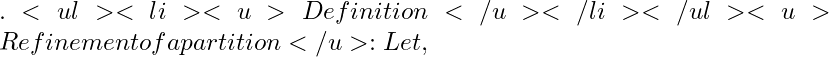
p_{2}
[a, b]
p_{1}subset p_{2} text{ and } delta(p_{1})leq delta(p_{2})
p_{2}
p_{1}
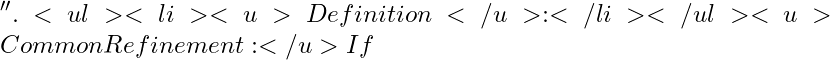
p_{2}
[a, b]
p_{1}subset p_{1}cup p_{2}
p_{2}subset p_{1}cup p_{2}
p_{1}cup p_{2}
p_{1}
p_{2}
p_{1}
p_{2}
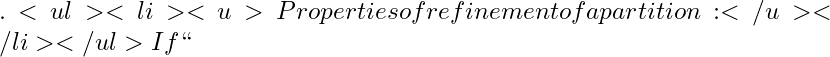
[a, b]
p_{1}, p_{2} in P [a,b]
p_{2}
p_{1}
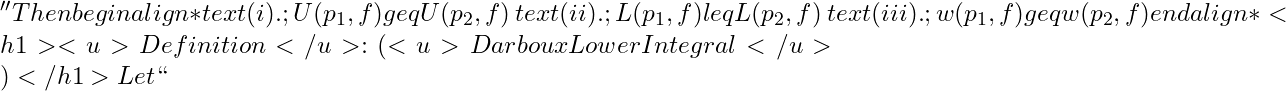
[a,b]
sup{lbrace L(p,f) : pin P [a,b]rbrace}
f
[a,b]
![Rendered by QuickLaTeX.com and denoted by [ int_{ubar{a}}^{b}f(x)dx ] <u>Darboux Upper Integral</u>: For real valued function ``](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-bd483d7ba560cf93828fd9af89bf2bae_l3.png)
[a, b]
inf{lbrace U(p,f) : pin P [a,b] rbrace}
f
[a, b]
![Rendered by QuickLaTeX.com and denoted by [ int_{a}^{bar{b}}f(x)dx ] <u>Particular fact</u>: For any real valued bounded function on](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9e799254634efd1be67bf376cc6f1573_l3.png)
p_{1}
p_{2}
[a, b]
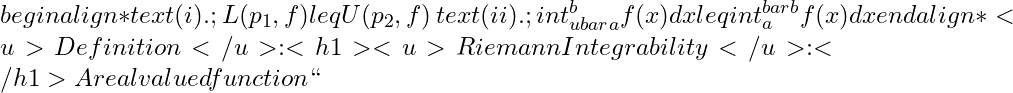
[a, b]
[a, b]
f
f
f in mathcal{R}[a,b]
f(x)=x,; xin[0,1]
f(x) in mathcal{R}[0,1]
[0, 1]n
p_{n}
[0, 1]
n
![Rendered by QuickLaTeX.com '' sub-intervals [I_{r}=left[ dfrac{r-1}{r},dfrac{r}{n} right], text{ for all } r=1,2,ldots,n text{ and } delta_{r}=dfrac{1}{n} text{ for every } r=1,2,ldots,n.] Here](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-61e44f42e8bda449c462ed8493b3b89b_l3.png)
[0, 1]
![Rendered by QuickLaTeX.com begin{align*} M_{r} & =dfrac{r}{n}, ;;;;;;; text{ for all } r=1,2,ldots,n,\ m_{r} & =dfrac{r-1}{n}, ;; text{ for all } r=1,2,ldots,n. end{align*} begin{align*} text{Then, } L(p_{n},f) &=sum_{r=1}^{n}m_{r}delta_{r}\ & =sum_{r=1}^{n}dfrac{r-1}{n}timesdfrac{1}{n}\ & =dfrac{1}{n^{2}}sum_{r=1}^{n}(r-1)\ & =dfrac{1}{n^{2}}times dfrac{(n-1)n}{2}\ L(p_{n},f) &=dfrac{1}{2}-dfrac{1}{2n}\ L(p_{n},f) &<dfrac{1}{2} end{align*} Also begin{align*} U(p_{n},f) &=sum_{r=1}^{n}M_{r}delta_{r}\ & =sum_{r=1}^{n}dfrac{r}{n}timesdfrac{1}{n}\ & =dfrac{1}{n^{2}}sum_{r=1}^{n}r\ & =dfrac{1}{n^{2}}times dfrac{(n+1)n}{2}\ U(p_{n},f) &=dfrac{1}{2}+dfrac{1}{2n}\ L(p_{n},f) &>dfrac{1}{2} end{align*} So, [sup{lbrace L(p_{n},f): nin mathbb{N}rbrace}=dfrac{1}{2}] [ int_{ubar{0}}^{1}f(x)dx=dfrac{1}{2} ] And [inf{lbrace U(p_{n},f): nin mathbb{N}rbrace}=dfrac{1}{2}] [ int_{0}^{bar{1}}f(x)dx=dfrac{1}{2} ] Here, [int_{ubar{0}}^{1}f(x)dx=int_{0}^{bar{1}}f(x)dx=dfrac{1}{2}] Hence, [f(x) in mathcal{R}[0,1]] And [int_{0}^{1}f(x)dx=dfrac{1}{2}] So, we understand by the example how we can use the definition of Riemann Integration. But for more complicated functions there will be difficulties to find maximum and minimum in every subinterval so, now we are going to modify the theory of ``when a function is said to be a Riemann integral.'' <u>Theorem :</u> let](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-359b180d2bc350c45ed625dad4dbb8d5_l3.png)
[a,b]
[a,b]
epsilon > 0 , exists text{ partition } P text{ of } [a,b]
![Rendered by QuickLaTeX.com such that [U(p,f)-L(p,f)<epsilon] <u>Proof : </u> (Necessary Part:) Let](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-18df99ee318640c81b729dd24acc797d_l3.png)
[a,b]
epsilon
f
[a,b]
epsilon
P
[a,b]
![Rendered by QuickLaTeX.com such that [L(p,f)>intlimits_{ubar{a}}^{b}f(x)dx-dfrac{epsilon}{2}=intlimits_{a}^{b}f(x)dx-dfrac{epsilon}{2}] Also [U(p,f)<intlimits_{a}^{bar{b}}f(x)dx+dfrac{epsilon}{2}=intlimits_{a}^{b}f(x)dx+dfrac{epsilon}{2}] Therefore [U(p,f)-L(p,f)<intlimits_{a}^{b}f(x)dx+dfrac{epsilon}{2}-intlimits_{a}^{b}f(x)dx+dfrac{epsilon}{2}=epsilon] Hence [U(p,f)-L(p,f)<epsilon] Conversely (Sufficient condition) Suppose for any positive number](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e112bbd75ccc65bf451c5d3c22c4bcc8_l3.png)
P
[a,b]
![Rendered by QuickLaTeX.com such that [U(p,f)-L(p,f)<epsilon] Since, [intlimits_{a}^{bar{b}}f(x)dxleq U(p,f)] and [intlimits_{ubar{a}}^{b}f(x)dxgeq L(p,f)] <u>A</u>lso [intlimits_{a}^{bar{b}}f(x)dxgeq intlimits_{ubar{a}}^{b}f(x)dx] Therefore [0leq intlimits_{a}^{bar{b}}f(x)dx-intlimits_{ubar{a}}^{b}f(x)dxleq U(p,f)-L(p,f) Hence Therefore [intlimits_{a}^{bar{b}}f(x)dx=intlimits_{ubar{a}}^{b}f(x)dx] Hence](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-05e10e4ea4cc16238a18586c218cbca7_l3.png)
[a,b]
f:[a,b] to mathbb{R}
[a,b]
{p_{n}}
[a,b]
{vert p_{n}vert}
![Rendered by QuickLaTeX.com converges to zero and [lim_{ntoinfty}lbrace U(lbrace p_{n}rbrace, f) - L(lbrace p_{n}rbrace, f)rbrace=0] Then](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-532fdde8aaa33dc76f72af325153f3c7_l3.png)
[a,b]
f:[0,1] to mathbb{R}
f(x) text{ on } [0,1]f(x)
[0,1]
nin mathbb{N}
left[dfrac{r-1}{n},dfrac{r}{n} right]r=1,2,ldots,n.
f[0,1]
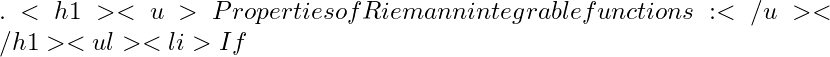
f in mathbb{R} [a,b]
f
f , : , [a,b]to mathbb{R}
f
f , : , [a,b]to mathbb{R}
[a,b]
f in mathbb{R} [a,b]
f , : , [a,b]to mathbb{R}
[a,b]
[a,b]
f(x)in mathcal{R}[0,1]
f , : , [a,b]to mathbb{R}
[a,b]
f
[a,b]
a<c<b
f , : , [a,b]to mathbb{R}
[a,c]
[a,b]
![Rendered by QuickLaTeX.com then</li> </ul> [int_{a}^{c}f(x)dx+int_{c}^{b}f(x)dx=int_{a}^{b}f(x)dx] <ul> <li>If](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-3a628bd2c78650d7ca62ec3db77b54dd_l3.png)
[a,b]
lambdainmathbb{R}
lambda f(x)
[a,b]
![Rendered by QuickLaTeX.com and further more,</li> </ul> [int_{a}^{b}lambda f(x)dx=lambdaint_{a}^{b}f(x)dx] <ul> <li>If](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-92e8ee8ca12532f71fe0b41557b50b14_l3.png)
[a,b]
f , : , [a,b]to mathbb{R}
g , : , [a,b]to mathbb{R}
lambda,mu in mathbb{R} ; lambda f(x)+mu g(x)
[a,b]
![Rendered by QuickLaTeX.com furthermore,</li> </ul> [int_{a}^{b}lbrace lambda f(x)+mu g(x)rbrace dx=lambdaint_{a}^{b}f(x)dx+muint_{a}^{b}g(x)dx] (x) If](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9506a4c7c107f0df7159f5e8a567e13a_l3.png)
[a,b]
vert f(x) vert
[a,b]
f(x)vert f(x)vert= 1;; forall x in [a,b]vert f(x)vert
[a,b]
f , : , [a,b]to mathbb{R}
g , : , [a,b]to mathbb{R}
[a,b]
fg
[a,b]
f , : , [a,b]to mathbb{R}
[a,b]
f^{2}
[a,b]
f , : , [a,b]to mathbb{R}g , : , [a,b]to mathbb{R}
g(x) geq k ; forall xin [a,b]
k>0
f/g
[a,b]
f , : , [a,b]to mathbb{R}
[a,b]
f(x) geq k ; forall xin [a,b]
k>0
1/f
[a,b]
I=[a,b]
J=[c,d]
f , : , Ito mathbb{R}
f , : , Jto mathbb{R}
f(I) subset [c,d]
gcirc f : Ito mathbb{R}
I
f:[0,1]to mathbb{R}
[0,1]
xto 0+ dfrac{1}{f(x)}toinfty +
dfrac{1}{f(x)}
[0,1]
dfrac{1}{f(x)}
[0,1]
f(x):[0,4]to mathbb{R}
f(x)[0,4]
f(x)
0leq f(x)<1x
[0,4]
f(x)
[0,4]
f(x)
[0,4]
x=1, x=2, x=3,
x=4
f(x)
[0,4]
f
[0,4]
f(x)
[0,4]
f(x)
[0,4]
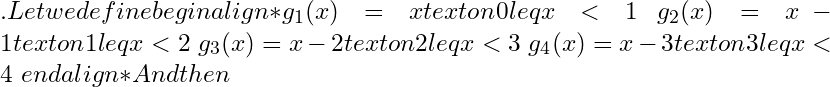
f(x):[0,4]to mathbb{R}f(x)
displaystyleint_{0}^{4}f(x)dx
displaystyleint_{0}^{4}f(x)dx=17
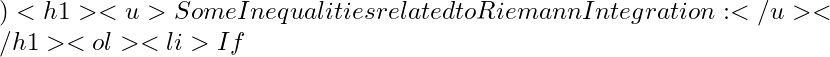
[a, b]
f(x)geq 0
x
[0, 1]
f:[a,b]to mathbb{R}g : [a,b]to mathbb{R}
[a, b]
f(x)geq g(x)
x
[0, 1]
![Rendered by QuickLaTeX.com .</li> </ol> Then [int_{a}^{b}f(x)dxgeq int_{a}^{b}g(x)dx] <ol start="3"> <li>If](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9863acd853dde90142ebd31e48921727_l3.png)
[a, b]
![Rendered by QuickLaTeX.com </li> </ol> Then [leftvertint_{a}^{b}f(x)dxrightvertleq int_{a}^{b}vert f(x)vert dx] <u>Problems related with these theories:-</u> <u> </u><u>Example.</u> Show that [dfrac{1}{2}leqint_{0}^{1}dfrac{dx}{sqrt{4-x^{2}+x^{3}}}leq dfrac{pi}{6} ] To prove this we are going to use all of the theories which we learnt till now, Let [g(x)=dfrac{1}{sqrt{4-x^{2}+x^{3}}}, xin[0,1] ] Here for all](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-41c84f184721e1317391c8b6a3908216_l3.png)
xin[0,1]
xin[0,1]xin[0,1]
xin[0,1]
![Rendered by QuickLaTeX.com <u>[f(x)geq g(x) geq h(x)]</u> So therefore [int_{0}^{1}f(x)dxgeq int_{0}^{1}g(x)dxgeq int_{0}^{1}h(x)dx] [int_{0}^{1}dfrac{1}{sqrt{4-x^{2}}}dxgeq int_{0}^{1}dfrac{1}{sqrt{4-x^{2}+x^{3}}}dxgeq int_{0}^{1}dfrac{1}{2}dx] [int_{0}^{1}dfrac{1}{2}dxleq int_{0}^{1}dfrac{1}{sqrt{4-x^{2}+x^{3}}}dxleqint_{0}^{1}dfrac{1}{sqrt{4-x^{2}}}dx] Now [int_{0}^{1}dfrac{1}{sqrt{4-x^{2}}}dx=left[sin^{-1}left(dfrac{x}{2}right)right]_{0}^{1}] ` [int_{0}^{1}dfrac{1}{sqrt{4-x^{2}}}dx=dfrac{pi}{6}] And [int_{0}^{1}dfrac{1}{2}dx=dfrac{1}{2}] Therefore [int_{0}^{1}dfrac{1}{2}dxleq int_{0}^{1}dfrac{1}{sqrt{4-x^{2}+x^{3}}}dxleqint_{0}^{1}dfrac{1}{sqrt{4-x^{2}}}dx] [dfrac{1}{2}leq int_{0}^{1}dfrac{1}{sqrt{4-x^{2}+x^{3}}}dxleqdfrac{pi}{6}] Hence proved. Now some work sheet problems:- <ol> <li>Let [f(x)=x^{2}, xin[0,1]]</li> </ol> Check](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c96998d05f9786d07b436cdd65401689_l3.png)
- Try to prove these problems
i) [dfrac{1}{3sqrt{2}}leq int_{0}^{1}dfrac{x^{2}dx}{sqrt{1+x}}leq dfrac{1}{3}]
- ii)
[dfrac{1}{2}left(1-dfrac{1}{e}right)leq int_{0}^{1}e^{-x^{2}}dxleq 1] iii) [dfrac{1}{3}leq int_{0}^{1}dfrac{x^{2}dx}{sqrt{1+x+x^{2}}}leq dfrac{pi}{4}]
- Try to show that
[int_{0}^{frac{pi}{2}}sin^{n+1}xdxleq int_{0}^{frac{pi}{2}}sin^{n} xdx ]
Bibliography
- Elementary Analysis: The theory of Calculus; Kenneth Ross.
- Improper Riemann Integration; Markos Roussos
- Modern Theories of Integration; H. Kestelman
- The Riemann Approach to Integration; Washek Pfeffer.
Thank you………

![Rendered by QuickLaTeX.com , Then, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e6e8086e2900853be37438a123232fee_l3.png" height="26" width="295" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[U(p,f)=sum_{r=1}^{n} M_{r} delta_{r}\]" title="Rendered by QuickLaTeX.com"/> <u>Lower Sum</u>: For the function ``](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e0d5f1a737b2d99bbed4f92eaf21f22b_l3.png)
![Rendered by QuickLaTeX.com , Then, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-a4455c31af7e203773cabd3580051fd9_l3.png" height="26" width="291" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[L(p,f)=sum_{r=1}^{n} m_{r} delta_{r}\]" title="Rendered by QuickLaTeX.com"/> <u> Facts:</u> <ol> <li>If](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-79e3af2ef886a5b2de0b777af423f4a8_l3.png)
![Rendered by QuickLaTeX.com is a constant function.</li> </ol> 2. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c7f0357709f1b56775c36d5ac8fa676d_l3.png" height="26" width="687" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[displaystyle U(p,f)-L(p,f)= sum_{r=1}^{n}( M_{r}delta_{r}-m_{r}delta_{r})\]" title="Rendered by QuickLaTeX.com"/> is the 'oscillatory sum' of ``](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2935a2863dbe2f0d643746431d61b6fd_l3.png)
![Rendered by QuickLaTeX.com , and we write that as <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-7e6582ca65984bd1addd6737cb8436e3_l3.png" height="26" width="295" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[w(p,f)= U(p,f)-L(p,f)\]" title="Rendered by QuickLaTeX.com"/> <ol start="3"> <li>For any bounded function ``](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-365d8156d9a544a93f429a0bf30dbcc8_l3.png)
![Rendered by QuickLaTeX.com ,</li> </ol> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-02e73fe8e5bff0946058e3cb035a238f_l3.png" height="26" width="448" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[m(b-a)leq L(p,f)leq U(p,f)leq M(b-a)\]" title="Rendered by QuickLaTeX.com"/> Where,](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1e0e3ed881e607c5ee5e999cfcb34baa_l3.png)
![Rendered by QuickLaTeX.com <u>Solution</u>: Let <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-0928069e46b35843d01f1f3b5ca65438_l3.png" height="23" width="703" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[p_{n}=leftlbrace 0,dfrac{1}{n},dfrac{2}{n},cdots , dfrac{2}{n} , 1 rightrbrace\]" title="Rendered by QuickLaTeX.com"/> be a partition of](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2aa30e75ed9db71d522d8aadbf1cfa40_l3.png)
![Rendered by QuickLaTeX.com be a function by <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-00c67ee0942dfa775948f0e59df18fa0_l3.png" height="30" width="771" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f(x)=begin{cases} x^{2}, ; x text{ x is rational }\ 1, ; x text{ is irrational} end{cases}\]" title="Rendered by QuickLaTeX.com"/> Here we are going to check the integrability of](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5a013b21f9c998f13842439c3256d461_l3.png)
![Rendered by QuickLaTeX.com we choose a partition <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-0928069e46b35843d01f1f3b5ca65438_l3.png" height="23" width="703" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[p_{n}=leftlbrace 0,dfrac{1}{n},dfrac{2}{n},cdots , dfrac{2}{n} , 1 rightrbrace\]" title="Rendered by QuickLaTeX.com"/> s [I_{r}=left[ dfrac{r-1}{r},dfrac{r}{n} right], text{ for all } r=1,2,ldots,n text{ and } delta_{r}=dfrac{1}{n} text{ for every } r=1,2,ldots,n.] [text{ Let } M_{r}=sup{leftlbrace f(x): xin left[dfrac{r-1}{n},dfrac{r}{n} right] rightrbrace} text{ for all } r=1,2,ldots,n.] [m_{r}=inf{leftlbrace f(x): xin left[dfrac{r-1}{n},dfrac{r}{n} right] rightrbrace} text{ for all } r=1,2,ldots,n.] Here](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-cc91d7f15d627036aba793691758b6db_l3.png)
![Rendered by QuickLaTeX.com So, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-4b29ca7af28916430e63c7fd7d48e976_l3.png" height="23" width="339" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[M_{r}=1 text{ for } r=1,2,ldots,n\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-7c1d27d87443146568a25439c03bc3f5_l3.png" height="26" width="446" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[m_{r}=(r-1/n)2 text{ for } r=1,2,ldots,n.\]" title="Rendered by QuickLaTeX.com"/> Then, begin{align*} U(p_{n},f) &=sum_{r=1}^{n}M_{r}delta_{r}\ & =dfrac{1}{n}sum_{r=1}^{n}1\ U(p_{n},f) &=1 end{align*} Also begin{align*} L(p_{n},f) &=sum_{r=1}^{n}m_{r}delta_{r}\ & =dfrac{1}{n^{3}}sum_{r=1}^{n}(r-1)^{2}\ & =dfrac{(n-1)(2n-1)}{6n^{2}} end{align*} Then <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-20a4da3b99020baf60a515cf1ee2878d_l3.png" height="27" width="805" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[lim_{ntoinfty}lbrace U(p_{n},f)-L(p_{n},f) rbrace=1-dfrac{1}{3}=dfrac{2}{3}neq 0.\]" title="Rendered by QuickLaTeX.com"/> Hence by the Remark we can say that](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2c7c887056a48c5845a5398ce8177aef_l3.png)
![Rendered by QuickLaTeX.com integrable. But the converse is not true. (Why?) <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-beb6a596eabcfad5b26bc87c53df092d_l3.png" height="26" width="959" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[text{Consider }f(x)=begin{cases} ;;; 1, ; x text{ x is rational }\ -1, ; x text{ is irrational} end{cases}\]" title="Rendered by QuickLaTeX.com"/> Here,](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-2a2ea9c1d1788e2a17251c9259727b99_l3.png)
![Rendered by QuickLaTeX.com but the converse is not true (try with the same function</li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-af991928da37d54f258329d347b013d1_l3.png" height="26" width="823" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f(x)=begin{cases} ;;; 1, ; x text{ x is rational }\ -1, ; x text{ is irrational} end{cases}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li>If](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-9230a38b5ac36b8a60cfaa62640ee556_l3.png)
![Rendered by QuickLaTeX.com defined by <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-c67b6a9199e71e7883f7e2236aa82908_l3.png" height="83" width="1841" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f(x)=begin{cases} 1, ;;;;;;;; x =0\ x, ; 0 Now we are going to check $ dfrac{1}{f(x)} $ is Riemann Integrable or not. Let's start:- Here $f:[0,1]to mathbb{R}$ is bounded function also $f$ is continuous on $[0,1]$ except $x=0$, so $f$ is Riemann Integrable on $[0,1]$. But\]" title="Rendered by QuickLaTeX.com"/>dfrac{1}{f(x)}=begin{cases} 1, ;;;;;;;; x =0\ dfrac{1}{x}, ; 0As](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-1690641259dc7d29053eedb3ab2e321a_l3.png)
![Rendered by QuickLaTeX.com such that <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-34c5f6ae35cb656a3db63c8d40c82166_l3.png" height="26" width="154" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f(x)=x-[x]\]" title="Rendered by QuickLaTeX.com"/> Here also we are going to check](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-f9692e2dcbf21cfdab375526a6db8abb_l3.png)
![Rendered by QuickLaTeX.com is <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8fc27a3fa559e3e5b828027b977ba8fd_l3.png" height="26" width="1063" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f(x)=begin{cases} x,& ;; 0leq x< 1\ x-1,& ; 1leq x<2\ x-2,& 2leq x <3\ x-3,& 3leq x <4\ 0,& x=4 end{cases}\]" title="Rendered by QuickLaTeX.com"/> Since](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8f16eaab8bdc0133e86a98e2710de33a_l3.png)
![Rendered by QuickLaTeX.com becomes <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-4baf3137848ca9b89e06ae8460b93827_l3.png" height="26" width="1137" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f(x)=begin{cases} g_{1}(x),& ;; 0leq x< 1\ g_{2}(x),& ; 1leq x<2\ g_{3}(x),& 2leq x <3\ g_{4}(x),& 3leq x <4\ 0,& x=4 end{cases}\]" title="Rendered by QuickLaTeX.com"/> Hence [int_{0}^{4}f(x)dx=int_{0}^{1}f(x)dx+int_{1}^{2} f(x)dx+int_{2}^{3} f(x)dx+int_{3}^{4} f(x)dx] Therefore we can do this now begin{align*} int_{0}^{4}f(x)dx & =int_{0}^{1}g_{1}(x)dx+int_{1}^{2} g_{2}(x)dx+int_{2}^{3} g_{3}(x)dx+int_{3}^{4} g_{4}(x)dx\ & =int_{0}^{1}xdx+int_{1}^{2}(x-1)dx+int_{2}^{3}(x-2)dx+int_{3}^{4}(x-3)dx\ & =dfrac{1}{2}+dfrac{1}{2}+dfrac{1}{2}+dfrac{1}{2}=2 end{align*} Therefore, [int_{0}^{4}f(x)dx=2] And we are done with this problem Now try this problem with same manner](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-0f76999175974544b9884b51f5197199_l3.png)
![Rendered by QuickLaTeX.com .</li> </ol> Then <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-81890e6ce439fdaf0c337a7fe69de2e6_l3.png" height="31" width="171" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[int_{a}^{b}f(x)dxgeq 0\]" title="Rendered by QuickLaTeX.com"/> <ol start="2"> <li>If](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-17349f84bca3d87324c5ab910f081848_l3.png)
![Rendered by QuickLaTeX.com <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-97cc1c0d0602688869b438ec14ed2c67_l3.png" height="29" width="170" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0leq x^{3}leq x^{2} leq 1\]" title="Rendered by QuickLaTeX.com"/> For all](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b2c73c90af9e4284111ece2cbed65666_l3.png)
![Rendered by QuickLaTeX.com <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-5176a402abe7c8f86566b94970f87172_l3.png" height="29" width="322" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0leq 4-x^{2}leq 4- x^{2}+ x^{3}leq 4,\]" title="Rendered by QuickLaTeX.com"/> For all](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-f2119f5d81a141b63dffe66f76b1ffda_l3.png)