The Quadratic Formula is primarily used to identify the roots (![]() -intercepts) of a quadratic function. What many people don’t know is that you can also easily find the vertex of the function by simply looking at the Quadratic Formula!
-intercepts) of a quadratic function. What many people don’t know is that you can also easily find the vertex of the function by simply looking at the Quadratic Formula!
Graphing Quadratic Functions
When graphing quadratic functions by hand, we will often use the quadratic formula to obtain the roots (or ![]() -intercepts) of the function. Then separately, we will work on finding the vertex of the function since this point defines the lowest (or highest) point on the graph, as well as the line of symmetry.
-intercepts) of the function. Then separately, we will work on finding the vertex of the function since this point defines the lowest (or highest) point on the graph, as well as the line of symmetry.
For the general quadratic function, ![]() , the quadratic formula identifies the roots at:
, the quadratic formula identifies the roots at:
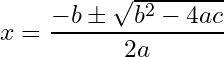
while the the vertex is found at 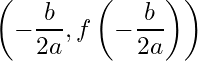 .
.
The ![]() -value of the vertex,
-value of the vertex, 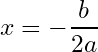 , is often referred to in algebra textbooks as The Vertex Formula.
, is often referred to in algebra textbooks as The Vertex Formula.
Finding the Vertex in the Quadratic Formula
Many people notice (or are taught) that the Vertex Formula can be found nestled in the Quadratic Formula. Specifically,
Less well known is the fact that the -coordinate of the vertex can also be obtained easily from the quadratic formula. The vertex of a quadratic function can be written as
where is the discriminant of the quadratic function. Recall that the discriminant of a quadratic function is
and it appears under the radical in the quadratic formula:
Also, notice that the denominator of the ![]() -coordinate and
-coordinate and -coordinate of the vertex are very similar. The
-coordinate’s denominator is just twice as big as the
![]() -coordinate’s!
-coordinate’s!
Now, let’s try out this idea and find the vertex of a quadratic from just the quadratic formula.
Example 1:
Suppose . Use the quadratic formula to identify the entire vertex of the function, and then verify the answer using the standard method.
Solution: The quadratic formula for this function is
The discriminant for this function is . So, the vertex should be at
Let’s double check our -coordinate by using the standard method (plugging
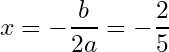
Example 2
Let’s try another example. Suppose . Identify the vertex using the quadratic formula, and verify the answer with the standard method.
Solution: The quadratic formula for this function is
The vertex should be 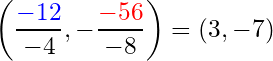
.
Again, we see the method works.
However, the savvy math student will immediately ask, “Does it work every time? Or was there something `special’ or `unusual’ about these particular quadratic functions?”
Does it Always Work?
This is an important question. In order to claim something is valid in mathematics, we have to do more than look at a few examples. We have to prove its validity. So, without further ado, here is the proof of this technique.
Given: The ![]() -coordinate of the vertex of a quadratic function is
-coordinate of the vertex of a quadratic function is 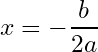 .
.
Show: The -coordinate of the vertex of a quadratic function is
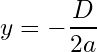
is the discriminant of the function.
Proof: Simply evaluate ![]() at
at 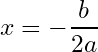 .
.
Well, how about that. It seems like any time we evaluate a quadratic at 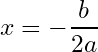 , we will end up with
, we will end up with .
So What?
So, what does this do for us in practical terms? Suppose we were asked to graph (by hand) the function . A good first step is to find the roots, and a good method for that is to use the quadratic formula.
Oops. This quadratic function doesn’t have real-valued ![]() -intercepts (Yes, it has complex roots, but that won’t help us graph, will it?).
-intercepts (Yes, it has complex roots, but that won’t help us graph, will it?).
But the function has a graph, we just have to find it. If only we had the vertex and one other point! Then we could graph the quadratic! But wait! We already have written out the quadratic formula, so that should tell us the vertex:
Now, together with the -intercept at
, we can easily plot the function.
Conclusion
In conclusion, the more we understand about the tools we have at our disposal, the easier it becomes to work through the mathematics that crop up in school and careers. And the more we learn, the more we become intrigued by the idea of other possibilities. I mean, doesn’t this insight into the quadratic formula just beg the question, “What else can we learn from the Quadratic Formula? Or the discriminant?”
© HT Goodwill and www.mathacademytutoring.com, 2016. Unauthorized use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to HT Goodwill and mathacademytutoring.com with appropriate and specific direction to the original content.

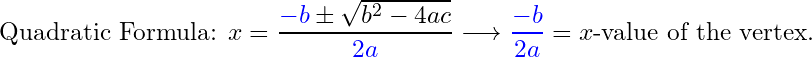
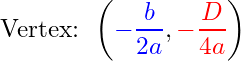
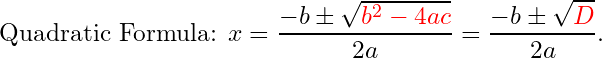
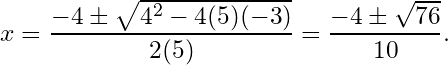
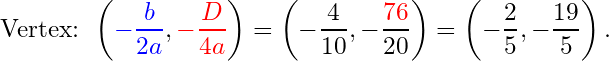
![Rendered by QuickLaTeX.com \begin{align*} f\left({\color{blue}{-\frac 2 5}}\right) & = 5\left({\color{blue}{-\frac 2 5}}\right)^2 + 4\left({\color{blue}{-\frac 2 5}}\right) - 3 && \mbox{Plugging in the $x$-value.}\\[6pt] & = 5\left(\frac 4 {25}\right) - \frac 8 5 - \frac 3 1 && \mbox{Simplifying.}\\[6pt] & = \frac 4 5 - \frac 8 5 - \frac{15} 5\\[6pt] & = \frac{-19} 5 && \mbox{$y$-value of the vertex.} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-dd49dcfac6cb2c87c9652fb32486d069_l3.png)
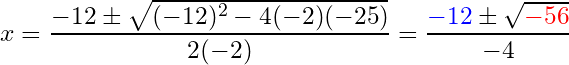
![Rendered by QuickLaTeX.com \begin{align*} f({\color{blue} 3}) & = -2({\color{blue} 3})^2 + 12({\color{blue} 3}) - 25\\[6pt] & = -2(9) + 36 - 25\\ & = -18 + 11\\ & = -7 \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-b83a75909bb52c56329532ec538a7cb7_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} f\left({\color{blue}{-\frac b {2a}}}\right) & = a\left({\color{blue}{-\frac b {2a}}}\right)^2 + b\left({\color{blue}{-\frac b {2a}}}\right) + c\\[6pt] & = a\left(\frac{b^2}{4a^2}\right) -\frac{b^2}{2a} + c && \mbox{Simplify a little.}\\[6pt] & = \frac{b^2}{4a} -\frac{b^2}{2a} + \frac c 1 && \mbox{Cancel the common factor.}\\[6pt] & = \frac{b^2}{4a} -\frac{2b^2}{4a} + \frac{4ac}{4a} && \mbox{Common denominator.}\\[6pt] & = \frac{-b^2 + 4ac}{4a} && \mbox{Combine numerators.}\\[6pt] & = -\frac{\color{red}{b^2 - 4ac}}{4a} && \mbox{Factor out a negative 1.}\\[6pt] & = -\frac{\color{red}{D}}{4a} \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-8e4b9e4476587a0a4271f50d2fa7bbc1_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} x & = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\[6pt] & = \frac{6 \pm \sqrt{(-6)^2 - 4(3)(8)}}{2(3)}\\[6pt] & = \frac{6 \pm \sqrt{-60}} 6 \end{align*}](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-3b96913df5dc7ecbfa0fa56d2359c8e1_l3.png)
![Rendered by QuickLaTeX.com \[% \mbox{Vertex: } \left(-\frac b {2a}, -\frac D {4a}\right) = \left(-\frac 6 6, -\frac{-60}{12}\right) = (1, 5). \]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-d1f684f9c59e028305c34112b305c3e8_l3.png)