We consider thus the functional notion of communication within the theory of dynamic systems, where the finite difference equation, or flow of a differential equation, is iterated upon as a function. Within this framework, there is a true underlying deterministic system which can be explained by a single function that is iterated upon over time as the repeated trials of the experiment. The space of outcomes may be partitioned, often into intervals, and then coded into a symbolic system of numerical sequences, where the place-order indicates the number of iterations of the function and the place-value the indexed interval it falls within [1]. This classifies initial conditions by their results, and may even represent a homomorphism between initial points and resulting codes.

Dysfunction

The proper functional notion of a probabilistic system is a dysfunction since it sends one state to many possible different states, in the sense that obtains an uncountably many values at 0 since analytically , i.e. the whole unit interval. We may study these as rather iterated functional recursions, where when there is a sensitive dependence upon initial conditions, we will likely find the function to be \textbf{hyperbolic} in that the derivatives of these iterates grow at least geometrically, and the problem of dysfunctionality will become one of imprecision in initial conditions.

From the previous lecture, a Markov chain is a dynamic system where, for n independent variables [2]. While the system may be \say{fully determined} by an initial condition , i.e. the exact (pre-partitioned) system at time t is given by , limits on the precision of measurement prevent us from ever either determining empirically or choosing an exact value to begin iterations upon . Thus, the secondary independent random variable , as post-partitioned, account for this error in measurement from imprecision.

Given a Partitioning of the space into a state-space . Let in that . Let be the index map as . communicate if , i.e. . is a function on the state-space in that . If our state-space is a dual space of functionals acting on the linear transformations of an underlying vector space, then has been well-defined.

Consider the modeling of a communication system. A message is sent through this system, arriving at a state of the system at each time. The message is thus the temporal reconfiguration chain of the system as it takes on different states from its possibility set . Due to noise in the message-propagation channel, i.e. the necessity of interpretation within any deciphering of \textit{the meaning} of the message from its natural ambiguity, we can only know the probability of the system’s state at a certain time, in that the full interpretation set of the message is a sequence of probability distributions as the probability of it having a certain state at a certain time. Performing this operation discretely in finite time, we can only sample the code as a sequence of states a number of trial-repetitions (), and take the frequency of each state at each time to be its approximate probability. We consider this to be empirical interpretation of the message. With possible states to our system, let be the symbolic code-space of all possible message sequences, including bidirectionally infinite ones, i.e. where the starting and finishing time is not known. Thus, a given empirically sampled message sequence is given by , where the is given by the frequency distributions .

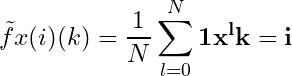
From the stochastic process approach, we might ask thus about the stationary distribution of these sampling codes, as what are the initial distribution conditions such that the distribution positions do not change over time? Let be the time iterational operation of the system on its space . While the times are counted , the length of each time step is given by , such that the real time is given by . 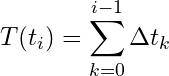The system at a given time is given by the probability distributions of the different states, which are the macro partitions of the micro states as thus . is the cumulative time distribution of the class-partitioned state-space distributions. The stationary distribution is such that .

Consider the string of numbers from N iterations of an experiment. What does it mean for the underlying numbers to be normally distributed? It means that the experiment is independent of time. The distribution stays the same at each time interval. Given a time-dependent process, the averages of these empirical measurement numbers will always be normal. Thus, normality is the stationary distribution of the averaging process. For random time-lengths, it averages all the values in that time-interval, without remembering the length of time or, equivalently, the number of values. markov – time homogeneity. Consider a system that changes states over time between different state-indexes . When the system-state appears as 0, we perform an average of the previous values between its present time and the previous 0 occurrence. Thus, the variable of 0 although an intrinsic part of the object of measurement is in fact a property of the subject performing the measurement, as when he or she decides to stop the measurement process and perform an averaging of the results. We call such a variable the basis when its objectivity depends upon a subjectivity in the action of measurement and the dynamics are given by the relationship between the occurrence of a 0 and the other states. Here 0 is the stopping time, where a string of results are thus averaged before continuing. Let , where gives the actual measured value from the state of the system. In reality, the system’s function time-inducing function has resulted in a particular value before it was partitioned into via , although here the time-inverting (dys)function determines this original pre-value from the result. Often the empirical is used from the average of the state’s values, i.e. , which thus takes the average value from an M-length self-communication string for a particular state. 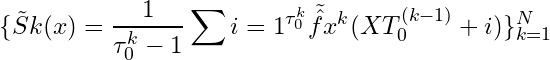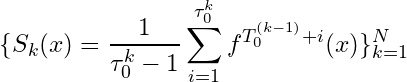& approach normal distributions as increases if state-0 is independent of the others.

References

1. Robert L. Devaney, An Introduction to Chaotic Dynamical Systems, 2nd Ed. Addison-Wesley Publishing Company, Inc, The Advanced Book Program, 1948.
2. Richard Serfozo, The Basics of Applied Stochastic Processes, Probability and its Applications. Springer-Verlag Berlin Heidelberg, 2009. p. 1.