The natural logarithm, whose symbol is ln, is a useful tool in algebra and calculus to simplify complicated problems. In order to use the natural log, you will need to understand what ln is, what the rules for using ln are, and the useful properties of ln that you need to remember.
What is the natural logarithm?
The natural logarithm is a regular logarithm with the base e. Remember that e is a mathematical constant known as the natural exponent. We write the natural logarithm as ln.
Since the ln is a log with the base of e we can actually think about it as the inverse function of e with a power.
or
The natural exponent e shows up in many forms of mathematics from finance to differential equations to normal distributions. It is clear that the logarithm with a base of e would be a required inverse so as to help solve problems involving such exponents.
Properties of ln
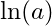 exists if and only if
exists if and only if 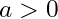
The natural logarithm of a requires that a is a positive value. This is true of all logarithms. This is an important parameter to remember, as any logarithm of a negative number is undefined.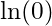 is undefined
is undefined
Notice how in property 1 that we define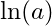 to exist if
to exist if 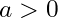 . That is no mistake. The logarithm of zero is undefined.
. That is no mistake. The logarithm of zero is undefined.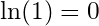
The natural logarithm of 1 is 0. This is a useful property to eliminate certain terms in an equation if you can show that the value in the natural logarithm is 1. It also serves as a divider between solutions of the natural log that are either positive or negative.if
and on the other side
if
.
The limit asas a approaches infinity is infinity. The natural logarithm is a monotonically increasing function, so the larger the input the larger the output.
Since the base of the natural logarithm is the mathematical constant e, the natural log of e is then equal to 1.
Since the natural logarithm is the inverse of the natural exponential, the natural log of e x becomes x.
Similar to property 6, the natural exponential of the natural log of x is equal to x because they are inverse functions.
The Natural Logarithm Rules
There are 4 rules for logarithms that are applicable to the natural log. These rules are excellent tools for solving problems with natural logarithms involved, and as such warrant memorization.The Product Rule
If you are taking the natural log of two terms multiplied together, it is equivalent to taking the natural log of each term added together.
Note 1: Remember property 1. The natural log of a negative value is undefined. This implies that both terms a and b from the product rule are required to be greater than zero.
Note 2: This property holds true for multiple terms:
The Quotient Rule
If you take the natural log of one term divided by another, it is equivalent to the natural log of numerator minus the natural log of the denominator.
Note 1: Remember property 1. The natural log of a negative value is undefined. This implies that both terms
The Reciprocal Rule
If you take the natural log of 1 divided by a number, it is equivalent to the negative natural log of that number.
The Power Rule
If you take the natural log of a term
It is of use to any student to be able to prove these 4 rules of natural logarithms. The observant student will see that the product rule can be proved easily using property 6 and 7, and some knowledge of exponents. The quotient, reciprocal, and power rule all follow from specific versions of the product rule. So if you are able to prove the product rule, the remaining three should be trivial.
Conclusion
- The natural log ln is a logarithm with a base of the mathematical constant e. ie
- The natural log ln is the inverse of e
- The 4 rules of logs

![Rendered by QuickLaTeX.com \[\ln\left(\frac{1}{x}\right)=-\ln(x)\]](https://www.mathacademytutoring.com/wp-content/ql-cache/quicklatex.com-e13168c0a575a3fcb23c3b1623d2b6be_l3.png)