Introduction to Algebraic Rings

An algebraic ring is one of the most fundamental algebraic structures. It builds off of the idea of algebraic groups by adding a second operation  (For more information please review our article on groups).

For rings we often use the notation of addition and multiplication because the integers are a good analogy for a ring, but the operations “+” and “⋅” do not necessarily represent addition and multiplication in the ring.

A ring is defined as a set S combined with two operations (“+” and “⋅”) that has the following properties:

I. The set S is a group under one operation (we will call this operation “+”):
a. It is closed under this operation: For all elements a and b in the set S, a+b is also in S.
b. It contains an additive identity element (which we will call “0”, although it does not necessarily represent the integer 0): There is some element 0 in the set S such that for every element a in S, a+0 = 0+a = a.
c. The operation is associative: For all a, b, and c in the set S, (a+b)+c = a+(b+c).
d. Inverses exist: For every element a in the set S, there is a (-a)  in S such that a+(-a)= (-a)+a = 0.

II. The group operation is commutative: For all a and b in the set S, a + b = b + a.
III. The second operation (written as “⋅”)

Follows these rules:
a. It is closed under this operation.
b. The set contains a multiplicative identity element (which we call “1”, although it does not necessarily represent the integer 1): such that for all elements a in the set S, a⋅1 = 1⋅a = a. c.

It is associative: For all a, b, and c in the set S, (a⋅b)⋅c = a⋅(b⋅c). d. It is distributive over “+” on both the right and left side: For all elements a, b, and c in the set S, a⋅(b+c) = a⋅b + a⋅c and (b+c)⋅a = b⋅a + c⋅a.

Note that inverses are not required for the “⋅” operation. If inverses do exist under “⋅”, we have a special kind of ring called a field.  

We will now look at some examples of rings and sets that aren’t rings.

Example 1.
The integers under addition and multiplication.

I. The integers are a group under addition (see our group article). I. Addition can be carried out in any order so it is commutative. III. Multiplication follows the additional rules laid out for rings. The integers are closed under multiplication. The identity element is 1. Multiplication is associative and it is also distributive.

Therefore, the integers are a ring under addition and multiplication. ∎ This is the reason addition, multiplication, 0, and 1 show up in our notation. If a set “acts like” the integers by following the ring axioms, it is a ring.

Example 2.
The set of 2×2 matrices under addition and multiplication.

I. The set of 2×2 matrices form a group under addition.
a. For any 2×2 matrices A and B, A+B is also a 2×2 matrix.
b. The additive identity “0” is the zero matrix .
c. Matrix addition is associative.
d. The additive inverse of a matrix A is just -A. Observe .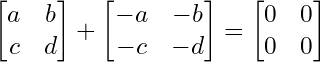

II. The addition of 2×2 matrices is commutative, A+B = B+A. III. Multiplication of 2×2 matrices satisfies the following conditions:
a. It is closed under the operation. The multiplication of two 2×2 matrices results in another 2×2 matrix.
b. The identity matrix is I = and for any 2×2 matrix A, A⋅I = I⋅A = A.
c. Matrix multiplication is associative. d. Matrix multiplication distributes over addition on the left and right side (This can be easily proven, but to save space it will not be proven here). Therefore, the set of 2×2 matrices is a ring.

Example 3.

The set of 2×2 matrices with non-negative entries under addition and multiplication. This set satisfies all of the requirements for the multiplication operation, but it is not a group under addition. Without negative entries, most matrices in this set do not have additive inverses.

Therefore, this set is not a ring. Like groups, rings do not have to be composed of real numbers or matrices. Some examples include sets of polynomials, the complex numbers, and integers modulo n. The word “ring” comes from the German word “Zahlring,” which means a collection of numbers that circle back on themselves.

However, now that the field has been studied more extensively, we know that cyclic rings are just one type of rings. The symbol ℤ for the integers is also named after a German word for numbers “Zahlen.”