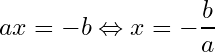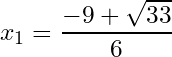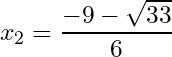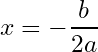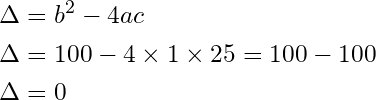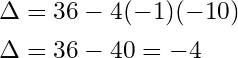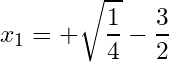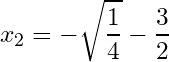How to Solve Equations of 1st, 2nd and 3rd Degree

by ms-academy | Jun 8, 2021 | Math Learning

Table of Contents

We may face the task of solving different types of equations while studying mathematics, so in this post, we will see how to solve first, second, and third degree equations.

Possible cases for the solutions

First, we need to understand what are the possible solutions for solving equations, here they are:

We define $S$ as the set of the possible solutions for the equation.

1-No solution: some equations don’t have a solution, i.e. there is no value possible for the variable to make the equation verified or true. Here is an example:

$3(x+2)=3x+10$

We simplify the equation by multiplying through the parentheses we get

$3x+6=3x+10$

and by subtracting $3x$ from both sides we get 6=10 which is false and therefore we deduce that there is no solution for this equation i.e. $S$ is empty $S=\lbrace\rbrace$ or $S=\emptyset$ .

2- Unique solution: equations may have a unique solution that verifies it, meaning that there is one and only one value for the variable to take to make the equation true. Here are some examples:

Example 1:

$3x+5=0$

by subtracting 5 from both sides, we get $3x=-5$

and by dividing by 3 both sides, we get $x=-\dfrac{5}{3}$

There it is the solution we are looking for 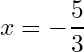$x=-\dfrac{5}{3}$ and it is unique. $-\dfrac{5}{3}$ is the only value for $x$ to make the equation true, $S=\left\lbrace-\dfrac{5}{3}\right\rbrace$ .

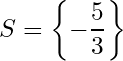
Example 2:

$7x-14=3x-6$

By subtracting $3x$ from both sides to eliminate the $3x$ on the right side of the equation we get

$4x-14=-6$

and by adding 14 to both sides we get $4x=8$ , by dividing by 4 we get $x=2$ , we get one and only one value for $x$ i.e. $S=\lbrace2\rbrace$ .

3- Multiple solutions: Equations may have multiple solutions, where there are several values for $x$ to verify the equation, here is an example of that:

$(2x+5)(x-3)=0$

we can do the multiplication of the parentheses and get

$2x^2-6x+5x-15=0$

$2x^2-x-15=0$

Using the factored writing of the equation, for the right side to be equal to 0, one of the two parentheses must equal 0 and for that we have two cases:

Either $2x+5=0$ by subtracting 5 we get $2x=-5$ and by dividing by 2 we get $x=-\dfrac{5}{2}$ ,

or $x-3=0$ and by adding 3 for both sides we get $x=3$ .

So we have two possible solutions for this equation 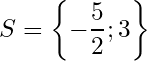$S=\left\lbrace-\dfrac{5}{2}; 3\right\rbrace$ .

4- Infinite solutions: An equation with infinite solutions is an equation always verified no matter the value of $x$ , let’s take a look at the following example:

$3x+5+2x+8=4(x+3)+x+1$

by simplifying both sides, we get

$5x+13=4x+12+x+1$

and then

$5x+13=5x+13$

by subtracting $5x$ from both sides we get $13=13$ .

By simplifying the equation we got to $13=13$ which is true all the time, it doesn’t depend on the value of $x$ , so no matter the value of $x$ the equation is always true, and since $x$ has infinite possible values we have infinite solutions for this equation.

Now, after seeing the different cases of the number of possible solutions, let’s see how to solve equations of first degree, second degree, and third degree.

Solving first degree equations

Definition

We call an equation of first degree every equation written like follows:

$ax+b=0$

Where $x$ is the variable and $a$ and $b$ are real numbers with $a$ different than 0.

Note that some equations of first degree are not on this form but after simplifying it always ends up with the form above.

We call it equation of first degree due to the variable $x$ begin up to power 1, and it is the highest power of the variable $x$ on the equation, meaning $ax^1+b=0$ .

Algebraic method

To solve an equation of first degree we first simplify it if it is not simplified to get to the form $ax+b=0$ and then all we need is pass b to the other side and divide by a, i.e.

$ax=-b \Leftrightarrow x=-\dfrac{b}{a}$

and there it is the solution of the equation $S=\left\lbrace-\dfrac{b}{a}\right\rbrace$

Example:

$8(x-1)-2(x+7)=3-x$

We simplify the equation

$8x-8-2x-14=3-x$

$7x=25$

then we get the form

$7x-25=0$

and the solution is $-\dfrac{b}{a}$ i.e. $S=\left\lbrace\dfrac{25}{7}\right\rbrace$ .

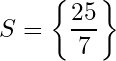
Geometric method

We can solve the equation geometrically by considering both sides of the equation as a straight line equation meaning the left side $y_1=ax+b$ is a line equation and the right side $y_2=0$ is a line equation.

Then we can draw both lines in an orthometric plane and we draw the line $y_1=ax+b$ and the line $y_2=0$ which is equivalent to the x-axis (because the x-axis is the line with $y=0$ )

$y_1=y_2$ (i.e. $ax+b=0$ ) means the point where the two lines intersect, so by drawing the line $ax+b$ and take the $x$ where it intersects with the x-axis we get our solution and it is the same as the algebraic method $S=\left\lbrace-\dfrac{b}{a}\right\rbrace$ .

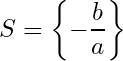
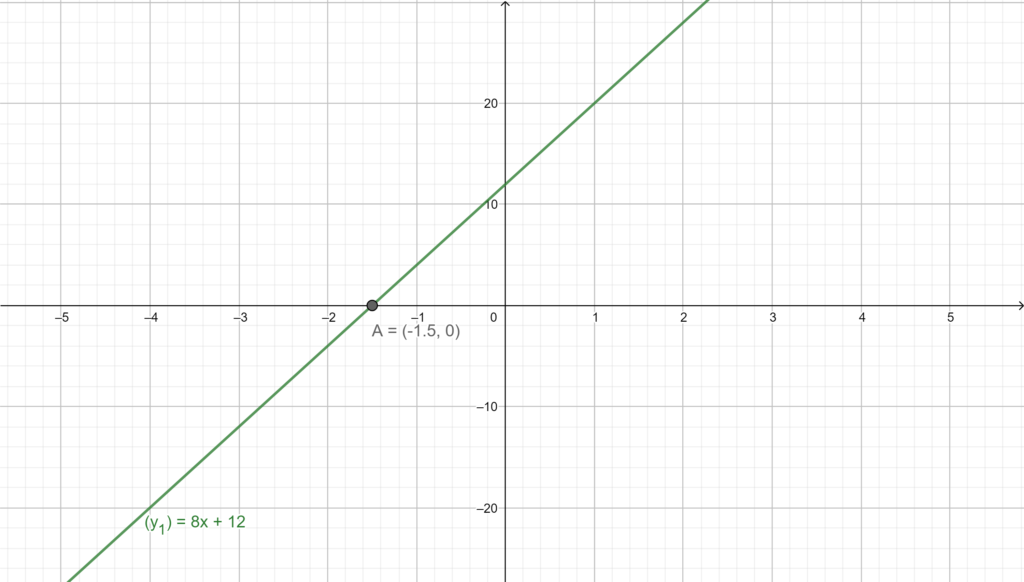
Example:

Let’s solve the equation $8x+12=0$

We draw the line with the equation $y_1=8x+12$

We pick 2 values of $x$ and get the respective value of $y$ and then we graph the two points in a plane and the new draw the line passing by the two points, and the $x$ coordinate of the point of intersection of the line $y_1$ and the x-axis is the solution of the equation.

Solving second degree equations

Definition

We call an equation of second degree, every equation with the standard form $ax^2+bx+c=0$ with $a$ , $b$ and $c$ being real numbers and $a$ different than zero. It is called a second degree equation because the highest power of $x$ in this equation is 2 (i.e. $x^2$ ).

Factoring to a multiplication of two first degree equations

A method to solve a second degree equation is to write it in the form of multiplication of two first degree equations and solving it by finding the solution for the two first degree equations.

How to factor a second degree equation?

If we consider a second degree equation like follow

$(x+a)(x+b)=x^2+(a+b)x+ab$

So, to get from the right side form to the left side factored form we need to figure out the values of $a$ and $b$ knowing the value of $(a+b)$ and $a\times b$ from the right side form. Let’s try an example:

$2x^2+20x+42=0$

We need to divide by 2 to remove the factor of $x^2$ and to get the form $x^2+(a+b)x+ab$

so, we get:

$x^2+10x+21=0$

Now with this form, we know that $a+b=10$ and $a\times b=21$ .

So, we need to find the two numbers $a$ and $b$ that their sum is equal to 10 and their product is equal to 21.

We have $a\times b=21$ and 21 can be written as product as $1\times 21$ or $3\times 7$ , and since $a+b$ must equal 10 we have $3+7=10$ , so the values of $a=3$ and $b=7$ are the ones that make $a+b=10$ and $a\times b=21$ .

After that, all we have to do is to write the equation in the form $(x+a)(x+b)$ .

so, we get:

$(x+3)(x+7)=0$

Now the resolution is straightforward since we have the product of two first degree equal to zero then we know for sure that either the first term of the product is equal to zero or the second is equal to zero, meaning either $(x+3)=0$ or $(x+7)=0$ , we solve each first degree term of the left side, we get:

$x+3=0 \Leftrightarrow x=-3$

$x+7=0 \Leftrightarrow x=-7$

and therefore we have the two solutions of the second degree equation $2x^2+20x+42=0$ , $S={-3;-7}$ .

We can verify by giving $x$ the value $-3$ or $-7$ , as follow:

$2\times (-3)^2+20\times (-3)+42=18-60+42=-42+42=0$

$2\times (-7)^2+20\times (-7)+42=98-140+42=-42+42=0$

Solving second degree equation using discriminant

We call the discriminant of the equation $ax^2+bx+c=0$ the expression $b^2-4ac$ , usually it is represented with the letter $\Delta$ , i.e. $\Delta=b^2-4ac$ .

Depending on the sign of discriminant we can determine the number and the value -if there is any- of the solutions, and the possible cases are the following:

1- If the discriminant is strictly positive ( $\Delta>0$ ), then the equation has two different solutions, and the solutions are:

$S=\left\lbrace\dfrac{-b+\sqrt{ \Delta}}{2a}; \dfrac{-b-\sqrt{\Delta}}{2a}\right\rbrace$ .

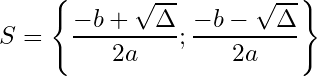
Example:

Let’s determine the solutions for the equation:

$3x^2+9x+4=0$

We evaluate $\Delta$ :

$\Delta=81-4\times 3\times 4=81-48=33$ so we have $\Delta>0$

We conclude that the equation has two distinct solutions, and they are the following:

$x_1=\dfrac{-9+\sqrt{ 33}}{6}$

$x_2=\dfrac{-9-\sqrt{33}}{6}$

$S=\left\lbrace\dfrac{-9+\sqrt{ 33}}{6}; \dfrac{-9-\sqrt{ 33}}{6}\right\rbrace$

2- If the discriminant is equal to zero, then the equation has one double root, meaning that the equation has two solutions that are the same so one repeated (or doubled) solution. The solution is given as follow:

$x=-\dfrac{b}{2a}$

Example:

Let’s determine the solutions for the equation:

$x^2+10x+25=0$

by evaluating $\Delta$ we get:

$\begin{align*} \Delta & =b^2-4ac\\ \Delta & =100-4\times 1\times 25=100-100\\ \Delta & =0 \end{align*}$

We conclude that the equation has one solution, and the solution is: 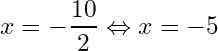$x=-\dfrac{10}{2} \Leftrightarrow x=-5$ ; $S=\lbrace-5\rbrace$ .

The reason why we call this solution a double root or repeated solution because the equation in fact can be written as the product of the same first degree polynomial, and therefore the same solution for the two first degree polynomials.

If we take the previous example, we have:

$x^2+10x+25=(x+5)(x+5)$

3-If the discriminant is strictly negative ( $\Delta<0$ ), then the equation has no solutions.

Example:

Let’s solve the equation

$-x^2+6 x-10=0$

by evaluating $\Delta$ we get:

$\begin{align*} \Delta & =36-4(-1)(-10)\\ \Delta & =36-40=-4 \end{align*}$

We have $\Delta<0$ , so we conclude that the equation has no solution (Because we can’t take the square root of delta since it’s negative).

Solving second degree equation using Algebraic Identities

In this method, we use the algebraic identity

$(x+k)^2=x^2+2kx+k^2$ ,

where $x$ is variable and $k$ is a real number.

To solve the equation $ax^2+bx+c=0$ , we follow these steps:

1- We divide both sides by $a$ , we get: $x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0$ .

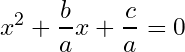
2- We subtract $\dfrac{c}{a}$ from each side, we get: $x^2+\dfrac{b}{a}x=-\dfrac{c}{a}$ .

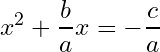
3- We add the value 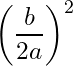$\left(\dfrac{b}{2a}\right)^2$ (i.e. the square of one half of $\dfrac{b}{a}$ ) to both sides, and we get:

$x^2+\dfrac{b}{a}x+\left(\dfrac{b}{2a}\right)^2=-\dfrac{c}{a}+\left(\dfrac{b}{2a}\right)^2$ .

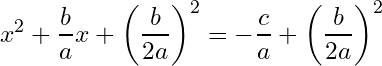
4- Now we have the left side is written as Expansion of the algebraic identity 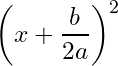$\left(x+\dfrac{b}{2a}\right)^2$ , so we can write the left side as follow:

$\left(x+\dfrac{b}{2a}\right)^2=-\dfrac{c}{a}+\left(\dfrac{b}{2a}\right)^2$ .

5- We square root both sides and solve the equation in hand.

For a better explanation, let’s use this method with an example:

$3x^2+9x+6=0$

First, we divide by 3, we get: $x^2+3x+2=0$ .

Second, we subtract 4 from both sides, we get: $x^2+3x=-5$ .

Third, we add the 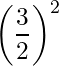$\left(\dfrac{3}{2}\right)^2$ to both sides, we get: $x^2+3x+\left(\dfrac{3}{2}\right)^2=-2+\left(\dfrac{3}{2}\right)^2$ .

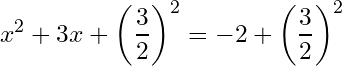
We simplify the right side:

$x^2+3x+\left(\dfrac{3}{2}\right)^2=-2+\dfrac{9}{4}$ ,

$x^2+3x+\left(\dfrac{3}{2}\right)^2=-\dfrac{8}{4}+\dfrac{9}{4}$ ,

$x^2+3x+\left(\dfrac{3}{2}\right)^2=\dfrac{1}{4}$ .

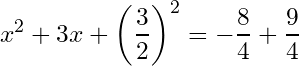
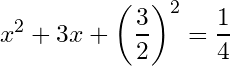
Forth, we write the left side as the algebraic identity, we get: 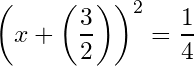$\left(x+\left(\dfrac{3}{2}\right)\right)^2=\dfrac{1}{4}$ .

Fifth, we take the square root of both sides, we get: 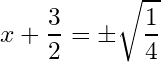$x+\dfrac{3}{2}=\pm\sqrt{\dfrac{1}{4}}$ .

Sixth, we subtract $\dfrac{3}{2}$ from both sides, we get: $x=\pm\sqrt{\dfrac{1}{4}}-\dfrac{3}{2}$ .

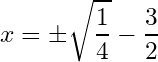
And therefore we have the two solutions of the second degree equation $3x^2+9x+6=0$ , the solutions are:

$x_1=+\sqrt{\dfrac{1}{4}}-\dfrac{3}{2}$

$x_2=-\sqrt{\dfrac{1}{4}}-\dfrac{3}{2}$

$S=\left\lbrace+\sqrt{\dfrac{1}{4}}-\dfrac{3}{2}; -\sqrt{\dfrac{1}{4}}-\dfrac{3}{2}\right\rbrace$ .

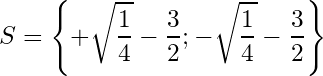
Solving geometrically

we can graph the function $f(x)=ax^2+bx+c$ and we look for which $x$ values $f(x)=0$ using graphing software or Graphing calculator.

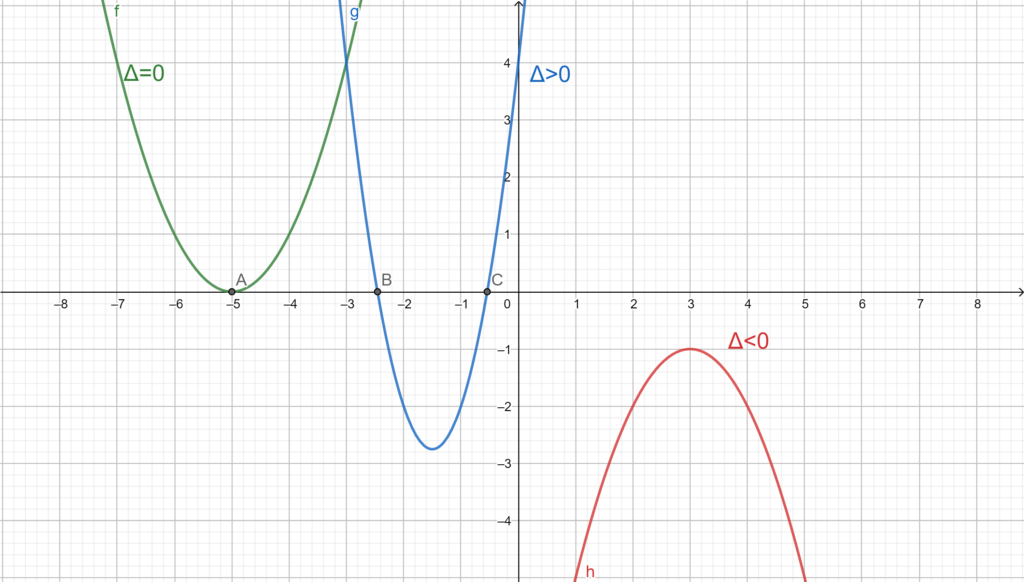
By graphing the function $f(x)=ax^2+bx+c$ , the graph we get is a parabola, solving the equation $ax^2+bx+c=0$ is equivalent to determine the value of $x$ for the intersecting points of the graph with the x-axis. There are three cases:

First, the graph intersects with the x-axis in two points, meaning the equations has two distinct solutions (correspond to the case where $\Delta>0$ ).
Second, the graph intersects with the x-axis at only one point, which means that the equation has one double solution (correspond to the case where $\Delta=0$ ).
Third, the graph doesn’t intersect with the x-axis, meaning the equation has no solutions (correspond to the case where $\Delta<0$ ).

The following figure shows the three possible cases:

Solving third degree equations

Definition

We call equation of third degree or cubic equation every equation when simplified has the following standard form:

$ax^3+bx^2+cx+d=0$

where $a$ , $b$ , $c$ , and $d$ are real numbers and $a$ different than 0.

It is called a third degree equation because the highest power of $x$ in this equation is 3 (i.e. $x^3$ ).

Solving third degree equation

For the number of possible solutions, unlike first and second degree equations, a third degree equation has at least one solution. Algebraically the reason is that the term with the highest power of $x$ , i.e. $x^3$ overgrow the rest of the terms and tend to infinity in both sides depending on the sign, meaning that for very small negative values for $x$ ( $x \rightarrow-\infty$ ) $x^3$ tend to $-\infty$ , and for very big positive values for $x$ ( $x \rightarrow+\infty$ ) $x^3$ tend to $+\infty$ (or the opposite is depending on the sign of the coefficient of the term $x^3$ ), that means going from one infinity to the other it passed by zero at least one time. There are three possible cases: one, two, or three solutions.

To solve a third degree equation, it would be helpful if we know one solution (or root) to start with. By knowing one solution (remember every cubic equation has at least one solution) we proceed by factoring the third degree equation into a product of a first degree polynomial (using the solution we know) with a second degree polynomial. At this point, we don’t know the coefficients of the second degree polynomial, so we find out their value and then we solve the second degree equation, and therefore we get the solutions of the third degree equation.

For a better understanding let’s try solving this equation:

$x^3+6x^2-x-30=0$

knowing that $x=2$ is a solution.

Since $x=2$ is a solution then the left side of the third degree equation can be factored into a product of first degree polynomial $(x-2)$ by a second degree polynomial $(ax^2+bx+c)$ , meaning that we can write the equation in the form:

$(x-2)(ax^2+bx+c)=0$

Now we need to find the values of $a,b$ and $c$ , in order to do that we use the first expanded form of the third degree polynomial, i.e.

$(x-2)(ax^2+bx+c)=x^3+6x^2-x-30$

by expanding the left side, we get:

$ax^3+bx^2+cx-2ax^2-2bx-2c=x^3+6x^2-x-30$

$ax^3+(-2a+b)x^2+(-2b+c)x-2c=x^3+6x^2-x-30$

Since both sides now are in the standard form, to figure out the values of $a,b$ , and $c$ . All we need to do is to equal each coefficient from the left to the correspondent coefficient from the right, in other words:

First, The coefficients of the term $x^3$ are equal i.e. $a=1$ .
Second, the coefficients of the term $x^2$ are equal i.e. $-2a+b=6$ .
Third, the coefficients of the term $x$ are equal i.e. $-2b+c=-1$ .
Fourth, the constants (coefficients of the term $x^0$ , meaning the real number without $x$ ) are equal i.e. $-2c=-30$ .

Now we determine the values of $a,b$ and $c$ :

So we have $a=1$

also $-2c=-30$ so $c=15$

we have $-2a+b=6$ , by replacing a with 1 we find $-2+b=6$ so $b=8$

Therefore, we have the values $a=1$ , $b=8$ , $c=15$ .

so the factored form is now as follow

$(x-2)(x^2+8x+15)=0$

Now all that is left is to solve the second degree equation $x^2+8x+15=0$

using any one of the methods we saw previously, we get two solutions $S=\lbrace-5;-3\rbrace$

Therefore, the third degree equation $x^3+6x^2-x-30=0$ has three distinct solutions $S=\lbrace-5; -3; 2\rbrace$ , and the equation can be written in the factored form

$(x-2)(x+3)(x+5)=0$ .

As we mentioned before, there are three possible cases for the number of solutions: one, two, or three solutions, and since we start with a known solution, it comes to the second degree polynomial to determine the number of solutions, and it goes as follow:

If the second degree polynomial has no solution then we have only one solution which is the one we started with.
In case the second degree polynomial has one solution (doubled root), then for the third degree equation we have a total of two solutions, the one that we started with and the one from the second degree polynomial.
If the second degree polynomial has two distinct solutions, then we have a total of three solutions, the one we started with plus the two from the second degree polynomial.

Notice that in case the constant $d$ in the standard third equation form is zero, meaning the equation is in the form

$ax^3+bx^2+cx=0$

we know that $x=0$ is a solution since each term has $x$

therefore, we don’t need to go through all the process to determine the second degree coefficients, we just take $x$ as a factor and we get our factored form as follow

$x(ax^2+bx+c)=0$

with $a,b$ , and $c$ already known and no need to determine them, so we proceed directly to solving the second degree equation.

Example:

let’s solve the equation

$x^3-8x^2+7x=0$

since there is no constant, we take $x$ as a factor

$x(x^2-8x+7)=0$

We know $x=0$ is a solution, so we proceed to solve the second degree equation $x^2-8x+7=0$

using one of the methods shown before we get two solutions $x=1$ or $x=7$ .

We conclude that the equation $x^3-8x^2+7x=0$ has three solutions $S=\lbrace0;1;7\rbrace$ , and the factored form is $x(x-1)(x-7)=0$ .

solving geometrically

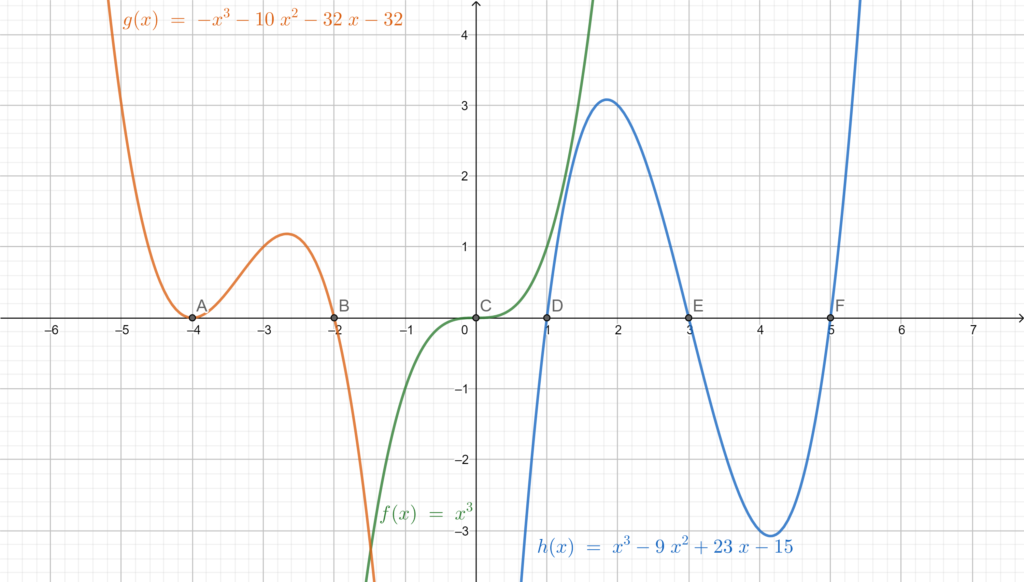
Geometrically, the reason why third degree equation has at least one solution is that the graph pass from $-\infty$ to $+\infty$ or the opposite (from $+\infty$ to $-\infty$ ), and therefore we are sure that the graph intersects with the x-axis at least one time.

To solve a third degree equation, we can graph the function $f(x)=ax^3+bx^2+cx+d$ and we look for which $x$ values $f(x)=0$ using graphing software or graphing calculator.

Solving the equation is equivalent to determine the value of $x$ for the intersection point of the graph and the x-axis. There are three possible cases:

The graph intersects only in one point with the x-axis, therefore the equation has only one solution.
The graph has two points of intersection with the x-axis, therefore the equation has two distinct solutions (one of them is doubled).
The graph intersects with the x-axis in three points, therefore the equation has three distinct solutions.

The following figure shows the different possible cases.

Conclusion

In conclusion knowing these solving methods can make the process of solving equations of first, second, and third degree equations straightforward, easier, and simpler with clear steps.

You want to have more fun! Check the graph below and see how the graphs change depending on the values of the coefficients. Check the type of equation you want to show (one or multiple), then slide to change the values of $a$ , $b$ , $c$ , and $d$ and watch the graphs change dynamically. Enjoy!

← PREVIOUS NEXT →

How to Solve Equations of 1st, 2nd and 3rd Degree

Possible cases for the solutions

Solving first degree equations

Definition

Algebraic method

Geometric method

Solving second degree equations

Definition

Factoring to a multiplication of two first degree equations

Solving second degree equation using discriminant

Solving second degree equation using Algebraic Identities

Solving geometrically

Solving third degree equations

Definition

Solving third degree equation

solving geometrically

Conclusion

Blog Main

Categories

Recent Posts

Archives

Archives

Categories

Meta