Limits of a Function: Operations and Properties – Calculus

by ms-academy | Sep 23, 2021 | Math Learning

Table of Contents

In the previous article: After introducing the idea of limits and how it helps to understand the behavior of the function on the ends of its domain of definition. In this article, we will see the limits of some known functions alongside the different properties and operations on limits.

Introduction

After learning about the idea of limits of a function when approaching the edges of its domain of definition and the different cases either when approaching a real number or when approaching infinity, and for easier manipulation and use, one very important next step is to learn about the properties and the different operations on limits which is the aim of this article where we will start with results of some known and commonly used functions and then we will learn some of the most important properties and the different arithmetic operations on limits. So, let’s get started!!!

Limits of some known functions:

Constant function:

$f(x)=c$ Domain: $D_{f}=\mathbb{R}$

$\lim_{x\rightarrow\pm\infty}f(x)=\lim_{x\rightarrow\pm\infty}c=c$

Identity function:

$f(x)=x$ , Domain: $D_{f}=\mathbb{R}$

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}x=-\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}x=+\infty$

The linear function:

$f(x)=ax+b$ , $a\neq 0$ Domain: $D_{f}=\mathbb{R}$

Depensing on the sign of $a$ , we distinguish two possible cases

If $a>0$ then

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}(ax+b)=-\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}(ax+b)=+\infty$

If $a<0$ then

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}(ax+b)=+\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}(ax+b)=-\infty$

The reverse function:

$f(x)=\dfrac{1}{x}$ , Domain: $D_{f}=\mathbb{R}^{*}=]-\infty;0[\cup]0;+\infty[$

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}\left(\dfrac{1}{x}\right)=0$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}\left(\dfrac{1}{x}\right)=0$

$\lim_{x\rightarrow 0^{-}}f(x)=\lim_{x\rightarrow 0^{-}}\left(\dfrac{1}{x}\right)=-\infty$

$\lim_{x\rightarrow 0^{+}}f(x)=\lim_{x\rightarrow 0^{+}}\left(\dfrac{1}{x}\right)=+\infty$

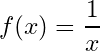
Polynomilal function of even degree:

A Polynomilal function of even degree is a function of the form $f(x)=a_{k}x^{2n}+a_{k-1}x^{2n-1}+\cdots+a_{1}x^{1}+a_{0}$

Domain: $D_{f}=\mathbb{R}$

We distinguish two possible cases:

Limits If $a_{k}>0$

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}a_{k}x^{2n}=+\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}a_{k}x^{2n}=+\infty$

Limits If $a_{k}<0$

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}a_{k}x^{2n}=-\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}a_{k}x^{2n}=-\infty$

Polynomilal function of odd degree:

A Polynomilal function of odd degree is a function of the form $f(x)=a_{k+1}x^{2n+1}+a_{k}x^{2n}+\cdots+a_{1}x^{1}+a_{0}$

Domain: $D_{f}=\mathbb{R}$

We distinguish two possible cases:

Limits If $a_{k+1}>0$

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}a_{k+1}x^{2n+1}=-\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}a_{k+1}x^{2n+1}=+\infty$

Limits If $a_{k+1}<0$

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}a_{k+1}x^{2n+1}=+\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}a_{k+1}x^{2n+1}=-\infty$

The exponential function:

$f(x)=e^{x}$ , Domain: $D_{f}=\mathbb{R}$

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}e^{x}=0$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}e^{x}=+\infty$

The logarithmic function:

$f(x)=\ln x$ , Domain: $D_{f}=\mathbb{R}^{+*}=]0;+\infty[$

$\lim_{x\rightarrow 0^{+}}f(x)=\lim_{x\rightarrow 0^{+}}\ln x=-\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}\ln x=+\infty$

The square root function:

$f(x)=\sqrt{x}$ , Domain: $D_{f}=\mathbb{R}^{+}=[0;+\infty[$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}\sqrt{x}=+\infty$

Operations on limits:

Let $f$ and $g$ be two functions, $a$ represents a real number or $+infty$ or $-infty$ . With the following tables, we will summarize the different possible cases of the arithmetic operations on limits.

Limit of the addition (or substraction) of two function:

$\lim_{x\rightarrow a}f(x)$	$l\in \mathbb{R}$	$l\in \mathbb{R}$	$l\in \mathbb{R}$	$+\infty$	$+\infty$	$-\infty$
$\lim_{x\rightarrow a}g(x)$	$l^{'}\in \mathbb{R}$	$+\infty$	$-\infty$	$+\infty$	$-\infty$	$-\infty$
$\lim_{x\rightarrow a}(f(x)+g(x))$	$l+l^{'}$	$+\infty$	$-\infty$	$+\infty$	Indeterminate	$-\infty$

Limit of the multiplication of two functions:

$\lim_{x\rightarrow a}f(x)$	$l\in \mathbb{R}$	$l>0$	$l>0$	$l<0$	$l<0$	$+\infty$	$+\infty$	$-\infty$	0	0
$\lim_{x\rightarrow a}g(x)$	$l^{'}\in \mathbb{R}$	$+\infty$	$-\infty$	$+\infty$	$-\infty$	$+\infty$	$-\infty$	$-\infty$	$+\infty$	$-\infty$
$\lim_{x\rightarrow a}(f(x)\times g(x))$	$l\times l^{'}$	$+\infty$	$-\infty$	$-\infty$	$+\infty$	$+\infty$	$-\infty$	$+\infty$	IDTRM	IDTRM

Limit of the division of two functions:

$\lim_{x\rightarrow a}f(x)$

$l\in \mathbb{R}$

$l$

$+\infty$

$-\infty$

$+\infty$

$-\infty$

$\lim_{x\rightarrow a}g(x)$

$l^{'}\in \mathbb{R}^{*}$

$+\infty$

$-\infty$

$l^{'}>0$

$l^{'}<0$

$l^{'}>0$

$l^{'}<0$

$+\infty$

$-\infty$

$+\infty$

$-\infty$

$\lim_{x\rightarrow a}\left(\dfrac{f(x)}{g(x)}\right)$

$\dfrac{l}{l^{'}}$

$+\infty$

$-\infty$

$+\infty$

IDTRM

Limits of polynomials function and rational functions on $+\infty$ and $-\infty$ :

The limit of a function of a polynomial function on $+\infty$ or $-\infty$ is the limit of its term of the highest degree on $+\infty$ or $-\infty$ respectively.

Example:

Let’s determine the limits of the function $f$ when $x$ tens to $+\infty$ or $-\infty$

we have the funxtion $f$ defined as follow:

$f(x)=-5x^{3}+2x^{2}-4x+1; \;\;\;\;\; D_{f}=\mathbb{R}$

We have:

$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}-5x^{3}=+\infty$

$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}-5x^{3}=-\infty$

The limit of a rational function, i.e. the quotient of two polynomials, on $+\infty$ or $-\infty$ is the limit of the quotient the terms of the highest degree of the two polynomials on $+\infty$ or $-\infty$ respectively.

Example:

Let’s determine the limits of the function $g$ when $x$ tens to $+\infty$ or $-\infty$

we have the funxtion $g$ defined as follow:

$g(x)=\dfrac{2x^{2}+3x+1}{x^{2}-1}; \;\;\;\;\; D_{f}=\mathbb{R}-\lbrace-1;1\rbrace$

If we calculate the limit of the function g on $+\infty$ the usual way we will get $\dfrac{+\infty}{+\infty}$ which is an indeterminate form, the same thing on $-\infty$ we get $\dfrac{-\infty}{-\infty}$ which is also an indeterminate form.

Instead, to avoid the indeterminate form, we determine the limit of the quotient of the highest degree term of each polynomial (for the numinator and for the denominator), and therefore we get:

$\lim_{x\rightarrow -\infty}g(x)=\lim_{x\rightarrow -\infty}\dfrac{2x^{2}}{x^{2}}=2$

$\lim_{x\rightarrow +\infty}g(x)=\lim_{x\rightarrow +\infty}\dfrac{2x^{2}}{x^{2}}=2$

Let’s take a look at the graph of the function $g$ and see how it looks like and compare it with the results we got!

Conclusion:

In this article, we discovered the different properties and operations on limits alongside how to determine the limits of polynomial and rational functions on infinity. Don’t miss the introduction article where we presented the idea of limits: Limit of a function: Introduction.

Also, if you want to learn more fun subjects, check out the post about Functions and some of their properties, or the one about How to solve polynomial equations of first, second, and third degrees!!!!!

And don’t forget to join us on our Facebook page for any new articles and a lot more!!!!!

← PREVIOUS NEXT →

Limits of a Function: Operations and Properties – Calculus

Introduction

Limits of some known functions:

Operations on limits:

Limits of polynomials function and rational functions on $+\infty$ and $-\infty$ :

Conclusion:

Blog Main

Categories

Recent Posts

Archives

Archives

Categories

Meta