Probability: Introduction to Probability Theory

by ms-academy | Oct 5, 2021 | Math Learning

Table of Contents

Introduction

Probability, or what is also called probability theory is a branch of mathematics, it is concerned with analyzing and evaluating the chances, occurrence, or the results of random events or phenomena; it also studies the laws that rule these events, of course, it is not possible to determine with certainty the outcome of a random event, but probability theory aims at estimating the chances of happening of the different possible outcomes.

It may also be defined or described as a way to mathematically study events that occur randomly by chance and the rules and laws that they follow.

Historically, the origin of the probability theory goes back to the 17th century, and it started with the interest in the games of chance (gambling) and the study of insurance, since then and with the contribution of many mathematicians the foundations of probability theory was set, revealing its importance and utility in various aspects of life and many different natural and social sciences such as mathematics (with its numerous branches like statistics, game theory, …etc.), Physics, Astronomy & Cosmology, Finance, Banking & Stock market, Computer science, Artificial intelligence, Machine learning, Chance games (sports events, lotteries, horse races, …etc.), and weather forecasting to name a few.

What is probability?

“A probability” means the chance of occurrence of a possible event. It has a value in the interval $[0,1]$ i.e. if we note the probability by $p$ , we have $0\leq p\leq 1$ ; here we have two special cases: the first is when $p$ is equal to 0, this means that there is no chance of occurrence of the event in consideration or in other terms “this event is impossible”; the second special case is when $p$ is equal to 1, which means that we are certain of the happening of the event in hand, or we can say “this event is certain” which implies also that any other possible event is impossible. although the probability is a value from the interval $[0,1]$ , it is often represented in a percentage form, for example, in the case where $p$ is equal to 0, we say that the chance of the happening of the event in hand is 0% i.e., it is impossible; in the case where $p$ is equal to 1, we can say that the chance of occurrence of the event is 100% ( $100\%=\dfrac{100}{100}=1=p$ ) i.e., the occurrence of the event is certain, this explains why the probability is always in the interval $[0,1]$ : 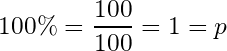we can’t have a chance less than “impossible” (i.e., $p=0$ ) and we can’t have a chance higher than “certainty” meaning we can’t be sure of the occurrence of an event more than 100% (i.e., $p=1$ ). For a random probability $p$ from the interval $[0,1]$ , all we need to do to convert the value of $p$ into the percentage form is to multiply it by 100 and add the percentage symbol “ $\%$ “, if we take as an example $p=0.6321$ then we can write the probability as $63.21\%$ . Therefore, we can conclude that if the value of $p$ is too close to 0 then we can say that this event is unlikely to occur, if the value of $p$ is close to 1 then we can say that the event is very likely to occur, and if the value of the probability $p$ is in the middle of the interval i.e., $p=0.5$ then the event has even chances of occurring or not.

So how do we calculate the probability of occurrence of an event?!

First, we need to know the total number of all the possible outcomes, and the number of the outcomes leading to the event (or in other terms the number of favorable outcomes)

After that, all we need to do is to follow the formula to determine a probability of an event given below

The probability of occurrence of an event

$P(E)= \dfrac{\text{The number of favorable outcomes}}{\text{The total number of outcomes}}$

Where can we find probability theory?

Well it is present either in an implicit manner or in a clear plain way in almost every field you can think about, here is a very short list that name a few:

Meteorology: This science is concerned with the study of the earth’s atmosphere and the prediction of the different weather conditions, utilize the gathered information on the weather conditions, and employ the already available data and patterns to determine the likelihood the different meteorological phenomena like precipitation, temperature, wind speed, and direction …etc.
For example, when we hear the weather network announce that the precipitation tomorrow is about 92% that means that we should carry umbrellas when we go out the next day.

Health care: Medical science uses extensively the probabilistic aspect in both research and treatment of the different medical cases. For example, if we take the research side, and if we look at the research in oncology for instance we clearly notice the importance of the probabilistic approach to determine the chances that a person gets cancer based on various studied factors that may increase or decrease the likelihood of getting cancer like age, antecedents and family history, lifestyle (smoking, drinking …) …etc. all these risk factors will be taken in consideration while calculating the chance of getting the sickness.

Another example which we all heard of it in the recent time, is the pharmaceutical industry which is responsible of the development and production of medication, and with the covid-19 pandemic, we saw an example of the probabilistic side of the industry specifically when each pharmaceutical producer of one of the vaccines announces the percentage of effectiveness, meaning the chance that the vaccine will work and that the person taking it will be protected from the virus.

Insurance sector: Knowing that the insurance sector is directly related to the happening of the different accidents and since accidents natural or human-made have are largely rules by randomness then the insurance companies base their insurance offers and rates on the likelihood of the customer having an accident (a car accident for example in the case of car insurance or a burned house in a forest wildfire in the case of home insurance …etc.). To do so, insurance companies use statistics and information about the different factors related to the insurance type that have any impact on increasing or decreasing the chance of accidents.

Sports: Sports are no exception to the use of the probabilistic approach, from teams to coaches and athletes to estimate chances of winning the game and to determine the best strategies to use in order to win the game or competition. To do so, players, coaches, and managers utilize the information from previous games and records for a better understanding of their strengths and weaknesses and to assure better performance in the next games.

Types of Probability

There are many types of probabilities, we cite here the three main ones:

Theoretical probability

This type of probability is based on the theoretical chances of occurrence of an event, or in other terms, it is based on the theoretically possible chances of something to happen. This kind of probability, as its name suggests, is mainly using reasoning to determine the probability of the happening of an event. An example of a theoretical probability is a toss of a coin: theoretically, we have the probability of getting “Head” is $P(\text{Head})=0.5$ (or $50\%$ ), and the probability of getting “Tail” is also $P(\text{Tail})=0.5$ (or $50\%$ ). so, the two events “Head” and “Tail” have the same probability of happening.

Experimental probability

This kind of probability, as the name suggests, isn’t just theoretical but experimental, it is based on the observations and the results coming from an experiment. For example, if we make the experiment of tossing a coin 20 times, and we get “Head” 13 times and “Tail” 7 times, this means, according to the results of the experiment, that the probability of getting “Head” is $P(\text{Head})=0.65$ (or $65\%$ ), and the probability of getting “Tail” is $P(\text{Tail})=0.35$ (or $35\%$ ). Notice that we took the same example as the one for the theoretical probability and yet we got a different probability based on experiment than the theoretical probability.

Axiomatic probability

The axiomatic probability has a set of rules called “Axioms”; these axioms apply always. There are three of them set by Kolmogorov also known as the “Kolmogorov’s three axioms”. The axiomatic type of probability and using Kolmogorov’s three axioms allow us to determine and calculate the chances of occurrence and non-occurrence of any given event.

The three axioms of Kolmogorov

Axiom 1: The probability of occurrence of an event $P(E)$ is greater or equal to 0: $P(E)\geq 0$
Axiom 2: Of the set of all possible events, the probability that at least one of them is going to occur is 1 (meaning we are certain that at least one of all the possible outcomes will happen).
Axiom 3: for any two events that are disjoint i.e., mutually exclusive, the probability of occurrence of either of them is equal to the addition of the probabilities of occurrence of each one of them. we can note as follow:
$\text{if } A\cap B=\emptyset \text{ then } P(A \cup B)=P(A)+P(B)$

Conclusion

This article was just an introduction to the branch of probability theory, presenting this field, defining what is probability, and introducing the different types of probabilities. Of course, there is no doubt we have a lot to learn about how to approach things from a probabilistic point of view, so don’t worry cause the probability of the coming of more fun articles is 1!!!

In the meantime, you can take a look at the sole articles about limits and infinity like Limit of a function: Introduction, Limits of a function: Operations and Properties, Limits of a function: Indeterminate Forms, or the one about Infinity: Facts, mysteries, paradoxes, and beyond!!!!!

Also, if you want to learn more fun subjects, check the post about Functions and some of their properties, or the one about How to solve polynomial equations of first, second, and third degrees!!!!!

And don’t forget to join us on our Facebook page for any new articles and a lot more!!!!!

← PREVIOUS NEXT →