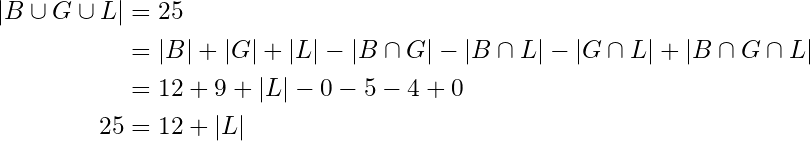Set Theory: Venn diagrams and Cardinality

by ms-academy | Oct 17, 2021 | Math Learning

Table of Contents

To continue with the introduction to Set theory, in this second article we will learn about Van diagrams, cardinality, and some of its properties.

Introduction:

After learning about the relations between sets and the operations on sets and their properties we will learn in this second article the representation of sets with the Van diagrams, we will also introduce the concept of cardinality and we’ll have a look at the importance and usage of set theory.

Quote: “A set is a Many that allows itself to be thought of as a One.” -Georg Cantor

Venn diagrams

A widely used way to visually represent sets and the relations between them is using Venn diagrams, this way of representing is named after the English mathematician and logician John Venn, who lived in the 18th century.

this way of representing the sets and the different relations between them is simple and easy to apply, we can summarize it as follow:

1-We draw a circle to represent a set, an ordinary one meaning not a universal one, inside the circle, we find the objects or elements of the set. The different circles representing the sets can overlap which means that these sets intersect.

Note that, a universal set is a set that contains all the elements that may be taken under consideration, in set theory to define the domain in which the operations on sets are done is to define the universal set. it is usually denoted $U$ .

Definition: We call a universal set the set of all the possible objects.

2-We draw a rectangle to represent the universal set, inside of it we find all subsets and elements.

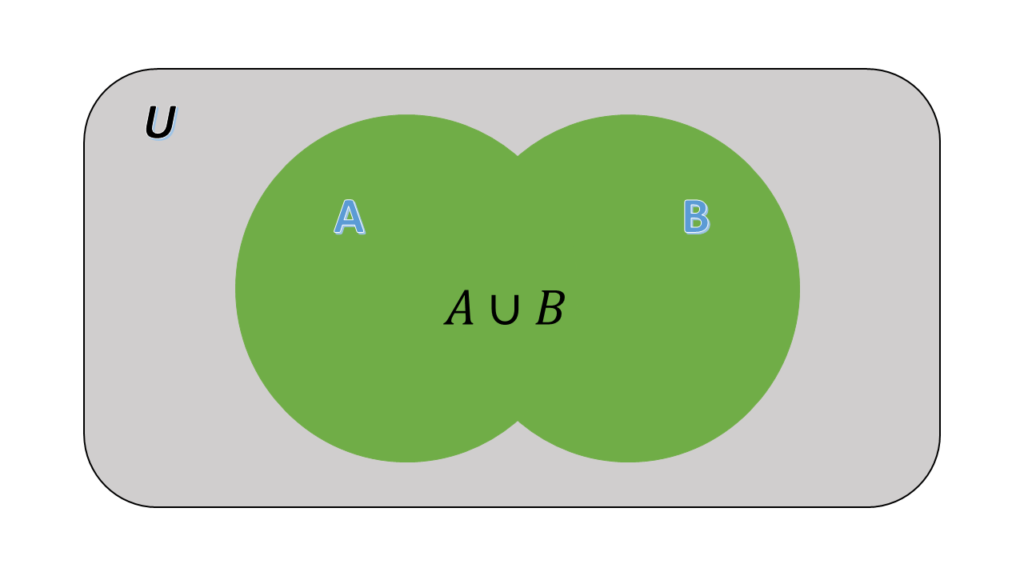
Here are some illustrations of the main operations on sets:

The union of $A$ and $B$ :
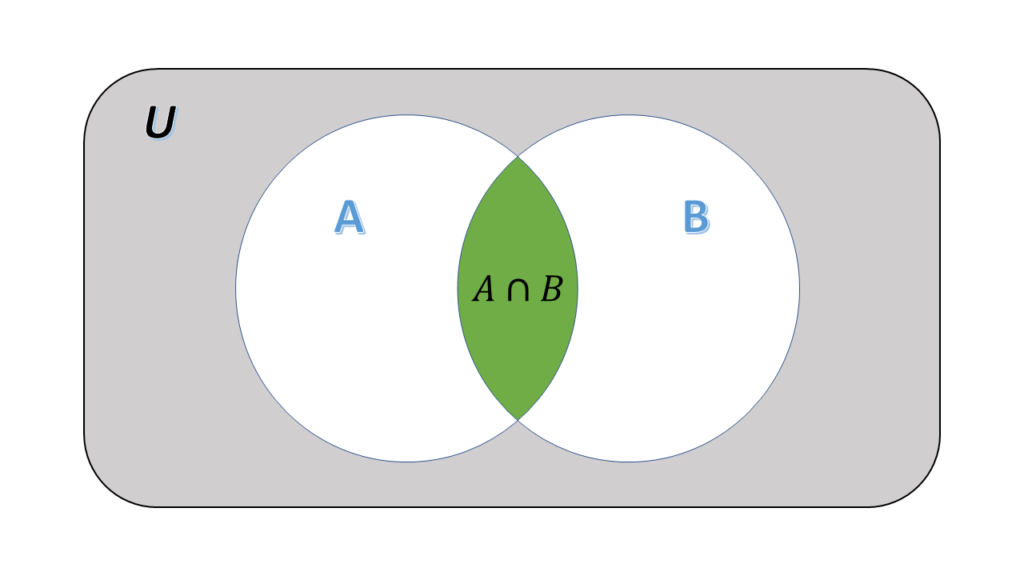
The intersection of $A$ and $B$ :

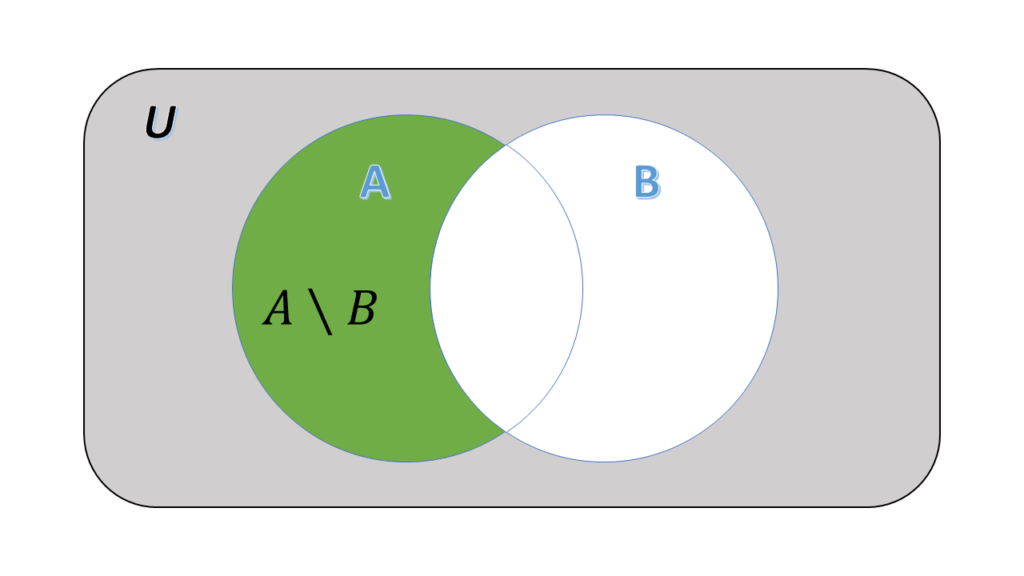
The difference of $A$ and $B$ :

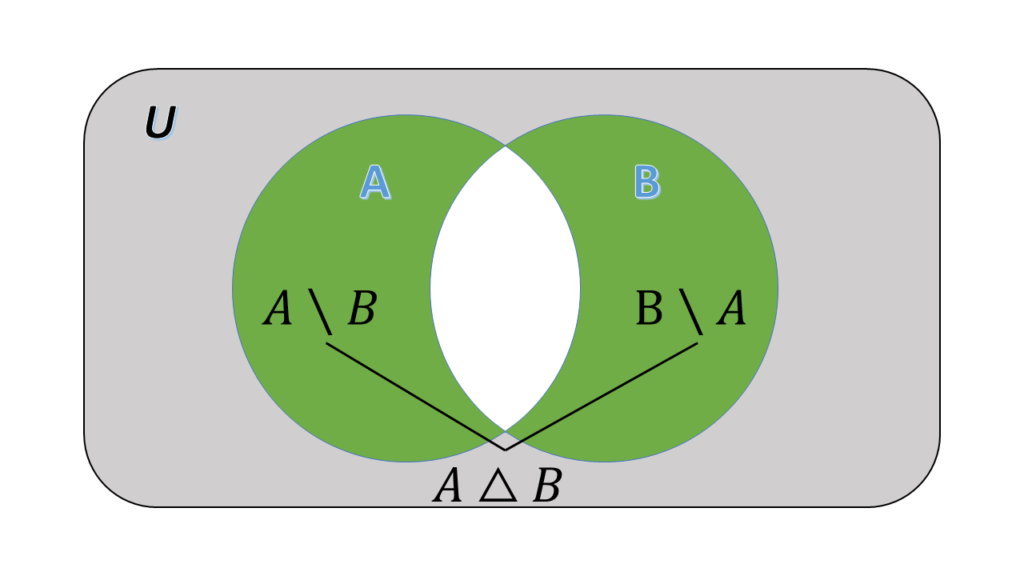
The Symmetric difference of $A$ and $B$ :

Cardinality of sets

A special and simple aspect of sets that mathematicians are always interested in, is the total number of distinct elements of a set whether it is a finite set or infinite. This property is very important since it allows us to know the size of a set and compare the different sets among many other things.

At the first look, this idea of cardinality is a very simple one we just need to count the elements of a given set to determine its cardinality, and that is totally true when we are dealing with finite sets, but the idea of cardinality isn’t that clear and simple to grasp when it comes to infinite sets and comparing the size of infinite sets!

The cardinality of a set $A$ is noted $\vert A\vert$ and sometimes in some references, it is noted by $Card(A)$ .

Note that the cardinality of the empty set $\emptyset$ is 0: $\vert \emptyset\vert =0$

Note also that we count only the distinct elements so for example, $\vert \lbrace 2,3,5,7,9,11,3,13,17,2,5\rbrace \vert =8$ .

First let’s take a look at some illustrating examples:

Example 1: Let the universal set be: $U=\lbrace 5,8,23,4,13,47,38,9,0\rbrace$ , and $A=\lbrace 0,4,5,8,9,13\rbrace$

Then we have the cardinality of the universal set $U$ is $\vert U\vert =9$ (meaning that $U$ has 9 distinct elements).

And the cardinality of $A$ is $\vert A\vert =6$ (meaning that $A$ has 6 distinct elements).

It makes sense that the cardinality of the universal set is greater (or equal) than any other one since any other one is a subset of the universal set.

Example 2: Let $B$ be defined as follow: $B=\lbrace n\in\mathbb{Z} \;\; :\;\; -10\leq n \leq 3\rbrace$

We have the cardinality of $B$ : $\vert B\vert =14$

(note that we can write $B$ in a different form such as: $B=\lbrace -10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3\rbrace$ ).

In case we have two sets $A$ and $B$ with the same cardinality we note $\vert A\vert =\vert B\vert$ and we say that $A$ and $B$ have the same size. Be careful between $\vert A\vert =\vert B\vert$ and $A=B$ ; $A=B$ means that $A$ and $B$ have exactly the same elements, for example, if $A=\lbrace 5,17,146,2,3\rbrace$ and $B=\lbrace 146,17,5,3,2\rbrace$ and then we have $A=B$ . For the expression $\vert A\vert =\vert B\vert$ it means the number of elements of $A$ is equal to the number of elements of $B$ but it doesn’t necessarily mean the same elements, for example, if $A=\lbrace4,7,9,11,62\rbrace$ and $B=\lbrace3,12,14,6,8\rbrace}$ we have $\vert A\vert =\vert B\vert$ but $A$ and $B$ have different elements.

Therefore, $A=B$ implies that $\vert A\vert =\vert B\vert$ but not the other way.

For the case of infinite sets, cardinality has some interesting properties, for example, we can have two infinite sets $A$ and $B$ and yet the number of elements of $A$ is bigger than the number of elements of $B$ i.e., $\vert A\vert >\vert B\vert$ ; this is a fundamental result of set theory for the study of limits and their properties. for more understanding check out our article about Infinity: Facts, mysteries, paradoxes, and beyond.

we can easily conclude that:

Every subset of a finite set is a finite
Every uperset of an infinite set is an infinite

Some properties of cardinality

let $A$ and $B$ be two sets, we have the following properties:

The sum of the cardinality of $A$ and the cardinality of $B$ is equal to the cardinality of the union of $A$ and $B$ :
$\vert A\vert +\vert B\vert =\vert A\cup B\vert$

The product of the cardinality of $A$ by the cardinality of $B$ is equal to the cardinality of the cartesian production of $A$ and $B$ :
$\vert A\vert. \vert B\vert =\vert A\times B\vert$

-Assuming the axiom of choice, we have the following result:

The cardinality of the union of $A$ and $B$ is equal to the cardinality of the cartesian product of $A$ and $B$ and it is equal to the maximum between the cardinality of $A$ and the cardinality of $B$ :

$\vert A\cup B\vert =\vert A\times B\vert =\text{Max}(\vert A\vert, \vert B\vert)$

For finite sets $A$ , $B$ and $C$ we have the following properties: The Inclusion-Exclusion principle:

For the case of two finite sets:
$\vert A\cup B\vert =\vert A\vert +\vert B\vert -\vert A\cap B\vert$

For the case of three finite sets:
$\vert A\cup B\cup C\vert =\vert A\vert +\vert B\vert +\vert C\vert -\vert A\cap B\vert -\vert A\cap C\vert -\vert B\cap C\vert +\vert A\cap B\cap C\vert$

Let’s take a look at an example for a better understanding of the Inclusion-Exclusion principle:

Suppose that at a birthday party we have the gests meet the following description:

We have 12 people wearing blue shirts and 9 people wearing green shirts;
5 guests have blue shirts and black jeans;
4 guests have black jeans and green shirts;
The total number of guests with a blue shirt or a green shirt or black jeans is 25.

And we want to determine the number of guests that have black jeans!

To answer this question, we take the following steps:

Let $B$ be the set of guests with blue shirts

Let $G$ be the set of guests with green shirts

Let $L$ be the set of guests with black jeans

Now using the notation, we can write the information given as follow:

$\vert B\vert =12$ ; $\vert G\vert =9$ ; $\vert B\cap L\vert =5$ ; $\vert L\cap G\vert =\vert G\cap L\vert =4$ ; $\vert B\cup G\cup L\vert =25$ .

we can safely assume that $B$ and $G$ are disjoint, meaning $\vert B\cap G\vert =0$ since guests are either wearing a blue shirt or a green one not both at the same time.

Now using the principle of Inclusion-Exclusion we get:

$\begin{align*} \vert B\cup G\cup L\vert & =25\\ & =\vert B\vert +\vert G\vert +\vert L\vert -\vert B\cap G\vert -\vert B\cap L\vert -\vert G\cap L\vert +\vert B\cap G\cap L\vert\\ & =12 + 9 +\vert L\vert - 0 - 5 - 4 + 0\\ 25 &=12+\vert L\vert \end{align*}$

Therefore $\vert L\vert =13$

So, the number of guests wearing black jeans is 13 (5 of them are wearing blue shirts and 4 of them are wearing green shirts and the rest (4 guests) are wearing neither a blue shirt nor a green one).

Examples of sets having equal cardinalities:

-The set of natural numbers $\mathbb{N}$ and the set of odd numbers $\mathbb{O}$ have equal cardinalities i.e. $\vert \mathbb{N}\vert =\vert \mathbb{O}\vert$ , and yet $\mathbb{O}$ is a subset of $\mathbb{N}$ ( $\mathbb{O}\subset \mathbb{N}$ )!

-The set of natural numbers $\mathbb{N}$ and the set of even numbers $\mathbb{E}$ have equal cardinalities i.e. $\vert \mathbb{N}\vert =\vert \mathbb{E}\vert$ , and yet $\mathbb{E}$ is a subset of $\mathbb{N}$ ( $\mathbb{E}\subset \mathbb{N}$ )!

-The set of natural numbers $\mathbb{N}$ and the set of integers $\mathbb{Z}$ have equal cardinalities i.e. $\vert \mathbb{N}\vert =\vert \mathbb{Z}\vert$ , and yet $\mathbb{N}$ is a subset of $\mathbb{Z}$ ( $\mathbb{N}\subset \mathbb{Z}$ )!

-The set of real numbers $\mathbb{R}$ and the interval of real numbers $]0,1[$ have the same cardinality, i.e. $\vert \mathbb{R}\vert =\vert]0,1[\vert$ , and yet $]0,1[$ is a subset of $\mathbb{R}$ ( $]0,1[\subset \mathbb{R}$ )!

-Any two open finite intervals of real numbers have equal cardinalities, i.e. $\vert ]a,b[\vert =\vert]c,d[\vert$ . For example, $\vert]0,1[\vert =\vert]5,13[\vert$ .

Conclusion

In this article we learned about the visual representation using Venn diagrams; we also learned about the concept of cardinality and some of its properties in the case of finite or infinite sets, and how it allows us by counting the number of distinct elements of sets, to compare their sizes either they are finite or infinite. This article shows a part of the importance of set theory and how it is fundamental for studying limits and comparing them, it is also fundamental for Algebra, logic, and probability theory among many other branches of mathematics and other sciences. Keep in mind that this is merely scratching the surface of set theory and that the set of things to learn about set theory has an infinite cardinality!!!!!

In the meantime, you can take a look at some articles about limits and infinity like Limit of a function: Introduction, Limits of a function: Operations and Properties, Limits of a function: Indeterminate Forms, or the ones about Infinity: Facts, mysteries, paradoxes, and beyond or check the one about Probability: Introduction to Probability Theory!!!!!

Also, if you want to learn more fun subjects, check the post about Functions and some of their properties, or the one about How to solve polynomial equations of first, second, and third degrees!!!!!

And don’t forget to join us on our Facebook page for any new articles and a lot more!!!!!

← PREVIOUS NEXT →

Set Theory: Venn diagrams and Cardinality

Introduction:

Venn diagrams

Cardinality of sets

Some properties of cardinality

Examples of sets having equal cardinalities:

Conclusion

Blog Main

Categories

Recent Posts

Archives

Archives

Categories

Meta